Вступ
У перших обчислювальних пристроях, що були прообразами сучасних комп’ютерів, важливу роль відігравали вибрані для них системи числення.
| Система числення - це правила запису чисел за допомогою спеціальних знаків - цифр, а також відповідні правила виконання дій з цими числами. |
Перші механічні лічильні машини (суматор Блеза Паскаля (1642 рік), лічильна машина Вільгельма Лейбніца (1673 рік), аналітична машина Чарлза Беббіджа (1848 рік) були створені на основі десяткової системи числення.
У 1938 році Конрад Цузе створив машину Z1, що була основана на принципах дії аналітичної машини Чарлза Беббіджа, але використовувала двійкову систему числення.
В сучасних комп’ютерах також використовується двійкова система числення і вся інформація зберігається у вигляді послідовностей нулів та одиниць.
Розглянемо принципи побудови основних систем числення, а також познайомимось із системами числення, що використовуються в комп’ютерах.
Непозиційні системи числення
Найпростіший спосіб порахувати, який використовує людина, - це «порахувати на пальцях». Один палець позначає одиницю (один день, одне дерево і т.д.).
Така система числення називається унарною - цифрами такої системи можуть використовуватися будь-які однакові предмети або символи (камінці, вузлики, засічки на дереві тощо).
За допомогою унарної системи числення можна записувати лише натуральні числа.
Натуральні числа - числа, що виникають природним чином при лічбі: 1, 2, 3, ... . Натуральні числа можна записувати за допомогою десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
|
Якщо використовувати унарну систему числення для запису великих чисел, то запис таких чисел виходить занадто довгим (уявіть собі, як записати тисячу чи, навіть, мільйон).
Наприклад, числа 1, 2, 3, 4, 5, ... будуть виглядати в унарній системі так:
1, 11, 111, 1111, 11111, ...Цифра будь-якої позиції числа, записаного в унарній системі числення, завжди позначає одиницю, тому унарна система відноситься до непозиційних систем числення.
| Непозиційна система числення - це система числення, в якій значення цифри у числі не залежить від позиції цієї цифри в записі числа. |
Ще однією непозиційною системою числення є римська система числення.
Ця система числення на сьогодні майже не застосовується, бо виконання арифметичних дій над багатозначними числами в цій системі дуже незручне.
Однак, її використовують для позначення століть, розділів і частин законів, томів видань, валентності хімічних елементів, а також з естетичною метою.
У Римській системі числення використовуються символи (літери латинської абетки)
I, V, X, L, C, D, MЗначення римських цифр:
-
I- один (1); -
V- п’ять (5); -
X- десять (10); -
L- п’ятдесят (50); -
C- сто (100); -
D- п’ятсот (500); -
M- тисяча (1000).
Римські цифри мають лише абсолютні значення і не мають позиційної значимості: I - це завжди 1, V - завжди 5, X - завжди 10 і т.д.
Натуральні числа записуються в Римській системі числення за допомогою повторення римських цифр, а загальне значення римського числа визначається шляхом додавання абсолютних значень його цифр. Наприклад:
VII = 5 + 1 + 1 = 7Тут символи V і I означають, відповідно, 5 і 1, незалежно від їх місця у числі.
В Римській системі числення існує ряд правил і обмежень запису чисел:
-
за допомогою класичної римської системи числення можна записувати лише натуральні числа в діапазоні
0-3999; -
неможливо записати дробові і від’ємні числа, а для запису великих чисел необхідно вводити додаткові цифри;
-
цифри
I,X,CіMможуть повторюватись, але не більше трьох разів, а цифриV,LіDповторюватись не можуть (дворазове повторення кожної з них дає значення, що позначається наступною старшою цифрою):
MMMDCCCLXXXVIII = 3888-
цифри
I,X,Cможуть передувати найближчій або наступній старшій цифрі, але не третій за порядком:IV,IX(але неIL),XL,XC(але неXDі неXM). При цьому вступає в дію принцип віднімання - значення меншої цифри віднімається від значення більшої:
IV = 5 - 1 = 4
IX = 10 - 1 = 9-
якщо поспіль йдуть однакові або й різні старші цифри, то молодша цифра може розміщуватися тільки передостанньою, наприклад:
XIX = 19
XXIX = 29
XXXIX = 39
XLIX = 49-
цифри
V,LіDне можуть розміщуватися перед найближчою старшою цифрою, так як отримане значення в цьому випадку дорівнює значенню, що позначають самі ці цифри. В результаті, наступні записи є некоректними:
VX
LC
DMПозиційні системи числення
Відомо, що цифри, якими ми користуємося для запису чисел, а саме 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, називаються арабськими. Але винайдені вони були в Індії! Чому ж тоді їх так називають?
В арабській системі числення використовують цифри
0, 1, 2, 3, 4, 5, 6, 7, 8, 9і ці ж цифри застосовуються для представлення чисел в десятковій системі числення.
Арабська система числення є позиційною системою числення.
| Позиційна система числення - система числення, в якій значення цифри залежить від позиції цифри у записі числа. |
| В позиційних системах числення значення, яке позначене цифрою в числі, залежить від позиції цифри в записі числа, а в непозиційних - значення цифри у числі не залежить від позиції цієї цифри в записі числа. |
Проілюструємо різницю у записі чисел в Римській і десятковій системах числення:
-
11- у такому записі перша одиниця позначає десять, а друга - один; -
II- тут обидві одиниці позначають одиницю; -
215,154,581- цифра5у першому випадку позначає5, у другому -50, а у третьому -500; -
XXV,XVII,VIII- в усіх записах чисел, де б не стояла цифраV, вона завжди позначає п’ять одиниць (іншими словами, величина, позначена символомV, не залежить від позиції цього символа в числі).
| Математичні дії в позиційних системах числення виконується легше, ніж у непозиційних, тому що здійснюються за нескладними алгоритмами (наприклад, множення в стовпець, порівняння двох чисел). |
У світі найбільш поширені саме позиційні системи числення. Поруч із знайомою усім десятковою системою числення, в комп’ютерній техніці широкого розповсюдження набули такі позиційні системи числення як двійкова, вісімкова та шістнадцяткова.
Позиційні системи числення мають ряд властивостей.
| Основа системи числення - кількість знаків (цифр), які використовуються для запису числа. |
Для запису чисел в позиційній системі з основою n необхідно мати алфавіт із n цифр. Зазвичай, для цього при n < 10 використовують n перших арабських цифр, а при n ≥ 10 - до десяти арабських цифр додають букви. Ось кілька прикладів алфавітів деяких позиційних систем:
| Основа | Назва | Алфавіт |
|---|---|---|
|
Двійкова |
|
|
Трійкова |
|
|
Вісімкова |
|
|
Шістнадцяткова |
|
Якщо необхідно вказати основу системи числення, в якій записане число, то вона прописується нижнім індексом для числа. Наприклад:
101112
2123
278
1716Позицію цифри у числі називають розрядом.
| Розрядність числа - кількість цифр, з яких складається число. |
Наприклад, 125 - трирозрядне число, 01110011 - восьмирозрядне число. Розряди нумеруються справа наліво і рахунок починається з 0.
Наприклад, в десятковому числі 1981:
-
остання цифра
1знаходиться в нульовому розряді (одиниці, 100); -
цифра
8знаходиться в першому розряді (десятки, 101); -
цифра
9- у другому розряді (сотні, 102); -
перша цифра
1- у третьому розряді (тисячі, 103).
Запис числа 1981 називається згорнутою формою запису числа. У загальному випадку, для довільного числа (цілого чи дробового - при цьому ціла частина відділяється від дробової комою, як ми звикли записувати, чи крапкою, як це відбувається в комп’ютерному системах), вона має вигляд:
aq = (an-1an-2…a1a0,a-1a-2…a-m)qУ цьому загальному вигляді згорнутої форми запису числа:
-
aq- вхідне число; -
q- основа системи числення; -
ai- цифри, які належать алфавіту даної системи числення; -
n- кількість розрядів цілої частини числа (нумерація розрядів починається з0справа наліво); -
m- кількість розрядів дробової частини числа (нумерація розрядів починається з1зліва направо і записується зі знаком-).
Нижні індекси визначають місце розташування цифри в числі (розряд):
-
додатні значення індексів - для цілої частини числа;
-
від’ємні значення індексів - для дробової частини числа.
Саме згорнутою формою запису числа ми і користуємося в повсякденному житті.
Десяткове число 1981 можна записати й у іншій формі
1981 = 1 · 103 + 9 · 102 + 8 · 101 + 1 · 100яка називається розгорнутою формою запису числа. Із цієї форми запису числа видно, що остання цифра 1 - це залишок від ділення вхідного числа на 10, число, складене з двох останніх цифр (81), - це залишок від ділення вхідного числа на 100 і т.д.
| Щоб визначити число, записане в позиційній системі числення, необхідно значення кожної цифри помножити на основу системи числення в степені, що дорівнює розряду цієї цифри, і додати отримані значення. |
Інший спосіб подання десяткового числа 1981 (не використовуючи операції піднесення до степеня) - за схемою Горнера :
1981 = ((1 · 10 + 9) · 10 + 8) · 10 + 1Якщо число 1981 позначити як a3a2a1a0, де a3, a2, a1 і a0 - окремі цифри, які розташовані в третьому, другому, першому і нульовому розрядах відповідно, і записати в системі числення q, то запис числа за схемою Горнера набуде загального вигляду:
a3a2a1a0 = ((a3 · q + a2) · q + a1) · q + a0Підсумовуючи, для запису довільного числа в позиційній системі числення з основою q розгорнута форма запису числа матиме наступний вигляд:
aq = ±(an-1qn-1 + an-2qn-2 + … + a0q0 + a-1q-1 + a-2q-2 + … + a-mq-m)Наприклад:
-
якщо
q = 10, то для числа1591,87210в десятковій системі числення кількість розрядівn = 4,m = 3; -
якщо
q = 2, то для числа1101,112у двійковій системі числення кількість розрядівn = 4,m = 2.
Розряди нумеруються з 0 справа наліво (для цілої частини числа) і з 1 зліва направо (для дробової частини числа). Тому в обох вказаних прикладах маємо для цілої частини числа кількість розрядів n = 4 (розряди 0, 1, 2, 3), а для дробової частини числа кількість розрядів m = 3 (розряди 1, 2, 3) і m = 2 (розряди 1, 2) відповідно.
|
Розгорнута форма запису числа дозволяє записувати будь-яке ціле або дробове (подається як сума цілої і дробової частин, будь-яка з цих частин може бути відсутня) невід’ємне число в заданій позиційній системі числення. Для позначення від’ємного числа використовується знак -, після якого, за тими самими правилами, записується модуль числа.
|
| Цілу і дробову частини, у записі дробового числа, завичай, розділяють символом «коми». Далі, в записі дробових чисел, будемо дотримуватися такого позначення, пам’ятаючи, що в комп’ютерних системах для цих речей використовується розділювач «крапка». |
| Схему Горнера і розгорнуту форму запису числа можна використовувати для перетворення числа із будь-якої системи числення в десяткову систему числення. |
Наведемо кілька прикладів, в яких використовуються вищезгадані форми запису чисел.
Отримаємо розгорнуту форму для десяткових чисел 23145 і 23,145:
2314510 = 2 · 104 + 3 · 103 + 1 · 102 + 4 · 101 + 5 · 100
23,14510 = 2 · 101 + 3 · 100 + 1 · 10-1 + 4 · 10-2 + 5 · 10-3Запишемо розгорнуту форму для чисел в різних системах числення: 1100112, 1213, 15FC16, 110,012:
1100112 = 1 · 25 + 1 · 24 + 0 · 23 + 0 · 22 + 1 · 21 + 1 · 20
1213 = 1 · 32 + 2 · 31 + 1 · 30
15FC16 = 1 · 163 + 5 · 162 + F · 161 + C · 160
110,012 = 1 · 22 + 1 · 21 + 0 · 20 + 0 · 2-1 + 1 · 2-2Усі числа із попереднього прикладу переведемо в десяткову систему за допомогою розгорнутої форми запису:
1100112 = 1 · 25 + 1 · 24 + 0 · 23 + 0 · 22 + 1 · 21 + 1 · 20 = 32 + 16 + 0 + 0 + 2 + 1 = 5110
1213 = 1 · 32 + 2 · 31 + 1 · 30 = 9 + 6 + 1 = 1610
15AF16 = 1 · 163 + 5 · 162 + A (10) · 161 + F (15) · 160 = 4096 + 1280 + 160 + 15 = 555110
110,012 = 1 · 22 + 1 · 21 + 0 · 20 + 0 · 2-1 + 1 · 2-2 = 4 + 2 + 0 + 0 + 0.25 = 6,2510| У прикладах вище, розгорнута форма запису була застосована до дробових чисел. Детальніше про дробові числа читайте у наступних розділах підручника, присвячених перетворенню дробових чисел і зберігання їх у пам’яті комп’ютера. |
Знаючи десяткове число і його запис в деякій позиційній системі числення, можна знайти основу цієї системи.
Наприклад, число 45 в деякій позиційній системі з основою x записується як 55x. Знайдемо основу цієї системи числення. Для цього запишемо це число в розгорнутій формі:
45 = 55x = 5 · x1 + 5 · x0 = 5 · x + 5Розв’язуючи рівняння 45 = 3 · x + 7 відносно невідомого x, отримаємо x = 8. Отже, шукана основа системи числення - 8 (вісімкова).
У складніших випадках може утворитися рівнняння 2-го або вищого степеня. Наприклад, візьмемо число 29, яке в деякій системі числення записується як 104x. Знайдемо основу цієї системи числення. Запишемо число в розгорнутій формі:
29 = 104x = 1 · x2 + 0 · x1 + 4 · x0 = x2 + 0 + 4Розв’язуючи рівняння
29 = x2 + 4відносно невідомого x, отримаємо два корені x1 = 5 і x2 = -5. Правильна відповідь 5, оскільки шукана основа системи числення має бути додатною.
Якщо ж запис числа в системі числення заданий не повністю, рішень може бути декілька. Наприклад, знайдемо усі основи систем числення, в яких запис десяткового числа 29 закінчується на 5. Використаємо схему Горнера, з якої слідує
29 = k · x + 5де x - невідома основа системи числення, k - деяке натуральне число або 0. Отже, з отриманого рівняння
24 = k · xможна визначити можливі значення основ систем числення - вони є дільниками числа 24. Таких дільників є 8: 1, 2, 3, 4, 6, 8, 12, 24. Оскільки, останньою цифрою у числі є 5, системи числення з основами 1, 2, 3, 4 нам не підходять, бо не мають в своєму алфавіті цифри 5. Тому, умові задачі задовільняють тільки основи 6, 8, 12, 24.
Знайдемо усі десяткові числа, які не більші за 28, запис яких в системі числення з основою 3 закінчується на 22. Використаємо схему Горнера, яка для нашої задачі матиме вигляд:
n = ((k · q + a1) · q + a0де n - шукані числа, k - деяке натуральне число або 0, q - основа системи числення (q = 3), a1 = 2, a0 = 2. Підставимо значення і отримаємо рівняння:
n = ((k · 3 + 2) · 3 + 2Після розкривання дужок
n = k · 32 + 2 · 3 + 2 = k · 9 + 8підставимо в рівняння значення k = 0, 1, 2, 3, 4,... і знайдемо відповідні числа n = 8, 17, 26, які задовільняють нашій умові (менше 28).
Основні поняття 2-3-8-10-16 систем числення
| Одне і те ж число можна подати у різних системах числення. Подання числа при цьому різне, а значення залишається незмінним. |
Коли пишуть ціле число, наприклад, 153, то використовують десяткову (за основою 10) систему числення.
Цифрами у десятковій системі є 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
|
«Всередині себе» комп’ютер використовує двійкову (за основою 2) систему числення.
Двійкова система числення містить тільки дві цифри, а саме 0 і 1.
|
Двійкові числа, як правило, значно довше їх десяткових еквівалентів.
Тому дві інші системи числення - вісімкова (за основою 8) і шістнадцяткова (за основою 16) - є дуже популярними, оскільки роблять зручним запис двійкових чисел.
У вісімковій системі використовуються цифри з діапазону від 0 до 7.
|
У шістнадцятковій системі виникає проблема запису чисел, оскільки тут потрібно шістнадцять цифр - найменша з яких 0 і найбільша зі значенням, еквівалентним десятковому числу 15 (на одиницю менше основи 16).
Для представлення шістнадцяткових чисел із значеннями від 10 до 15 (в десятковому еквіваленті) домовилися використовувати літери від A до F.
|
Так, у шістнадцятковому представленні можна написати, наприклад, число 584, що має десятково-подібний вигляд і містить тільки цифри, або число 459DD5, що містить цифри і літери, або число FFF, що складається лише з літер.
| Двійкові цифри | Вісімкові цифри | Десяткові цифри | Шістнадцяткові цифри |
|---|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
|
3 |
3 |
3 |
|
4 |
4 |
4 |
|
5 |
5 |
5 |
|
6 |
6 |
6 |
|
7 |
7 |
7 |
|
8 |
8 |
||
9 |
9 |
||
A (десяткове значення 10) |
|||
B (десяткове значення 11) |
|||
C (десяткове значення 12) |
|||
D (десяткове значення 13) |
|||
E (десяткове значення 14) |
|||
F (десяткове значення 15) |
| Атрибут | Двійкова система | Вісімкова система | Десяткова система | Шістнадцяткова система |
|---|---|---|---|---|
Основа |
2 |
8 |
10 |
16 |
Найменша цифра |
0 |
0 |
0 |
0 |
Найбільша цифра |
1 |
7 |
9 |
F |
| У кожній із зазначених систем числення використовується позиційна нотація - кожне місце, на якому стоїть цифра, має різне позиційне значення. Тому такі системи числення є позиційними. |
Ще раз нагадаємо особливості позиційних систем числення у наведених нижче прикладах.
Наприклад, у десятковому числі 628 (цифри 6, 2 і 8 називають символьними значеннями), говорять, що цифру 8 записано в позиції одиниць, 2 - в позиції десятків, 6 - в позиції сотень.
Кожна з цих позицій є відповідним степенем основи 10; ці степені починаються з 0 і збільшуються на 1 в міру переміщення вліво вздовж числа.
Десяткова цифра |
6 |
2 |
8 |
Ім’я позиції |
Сотень |
Десятків |
Одиниць |
Позиційне значення |
100 |
10 |
1 |
Позиційне значення як степінь основи (10) |
102 |
101 |
100 |
Для великих десяткових чисел такими позиціями зліва будуть позиції:
-
тисяч (103)
-
десятків тисяч (104)
-
сотень тисяч (105)
-
мільйонів (106)
-
десятків мільйонів (107)
-
і т.д.
У двійковому числі 101 видно, що крайня права одиниця записана в позиції одиниць, 0 знаходиться в позиції двох і крайня ліва одиниця в позиції чотирьох. Зауважимо, що кожна з цих позицій є степенем основи (числа 2); ці степені починаються з 0, збільшуючись на одиницю відповідно до зміни по числу вліво.
Двійкова цифра |
1 |
0 |
1 |
Ім’я позиції |
Чотирьох |
Двох |
Одиниць |
Позиційне значення |
4 |
2 |
1 |
Позиційне значення як степінь основи (2) |
22 |
21 |
20 |
Для великих двійкових чисел такими позиціями зліва будуть позиції:
-
восьми (23)
-
шістнадцяти (24)
-
тридцяти двох (25)
-
шістдесяти чотирьох (26)
-
і т.д.
Для вісімкового числа 425 говорять, що цифра 5 записана в позиції одиниць, 2 - в позиції восьми і 4 - в позиції шістдесяти чотирьох. Зауважимо, що кожна з цих позицій є степенем основи (числа 8); ці степені починаються з 0, збільшуючись на одиницю відповідно до зміни по числу вліво.
Вісімкова цифра |
4 |
2 |
5 |
Ім’я позиції |
Шістдесяти чотирьох |
Восьми |
Одиниць |
Позиційне значення |
64 |
8 |
1 |
Позиційне значення як степінь основи (8) |
82 |
81 |
80 |
Для великих вісімкових чисел наступними зліва будуть позиції:
-
п’ятсот дванадцяти (83)
-
чотирьох тисяч дев’яноста шести (84)
-
тридцяти двох тисяч семисот шістдесяти восьми (85)
-
і т.д.
Для шістнадцяткового числа 3DA говорять, що A знаходиться в позиції одиниць, D - в позиції шістнадцяти і 3 - в позиції двохсот п’ятдесяти шести. Зауважимо також, що кожна з цих позицій є степенем основи системи числення (числа 16); ці степені починаються з 0, збільшуючись на одиницю відповідно до зміни по числу вліво.
Шістнадцяткова цифра |
3 |
D |
A |
Ім’я позиції |
Двохсот п’ятидесяти шести |
Шістнадцяти |
Одиниць |
Позиційне значення |
256 |
16 |
1 |
Позиційне значення як степінь основи (16) |
162 |
161 |
160 |
Для довгих шістнадцяткових чисел наступними зліва будуть позиції:
-
чотирьох тисяч дев’яноста шести (163)
-
шістдесяти п’яти тисяч п’ятсот тридцяти шести (164)
-
і т.д.
| Основне застосування вісімкових і шістнадцяткових чисел в комп’ютерних обчисленнях полягає в скороченні довжини запису двійкового представлення чисел. |
Таблиця нижче демонструє, як великі двійкові числа можна записати в дуже короткій, стислій формі в системах числення з більшими основами, ніж двійкова система.
| Десяткове число | Двійкове представлення | Вісімкове представлення | Шістнадцяткове представлення |
|---|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
2 |
10 |
2 |
2 |
3 |
11 |
3 |
3 |
4 |
100 |
4 |
4 |
5 |
101 |
5 |
5 |
6 |
110 |
6 |
6 |
7 |
111 |
7 |
7 |
8 |
1000 |
10 |
8 |
9 |
1001 |
11 |
9 |
10 |
1010 |
12 |
A |
11 |
1011 |
13 |
B |
12 |
1100 |
14 |
C |
13 |
1101 |
15 |
D |
14 |
1110 |
16 |
E |
15 |
1111 |
17 |
F |
16 |
10000 |
20 |
10 |
Вибір системи числення для подання чисел у пам’яті комп’ютера має бути зваженим кроком.
В разі вибору системи числення, зазвичай, враховуються такі вимоги, як надійність подання чисел при використанні фізичних елементів, економічність (використання таких систем числення, в яких кількість елементів для подання чисел із деякого діапазону була б мінімальною).
Наприклад, для запису цілих чисел від 1 до 999 у десятковій системі числення достатньо трьох розрядів, тобто трьох елементів. Оскільки кожен елемент може перебувати в десятьох станах, то загальна кількість станів - 30, у двійковій системі числення 99910 = 11111001112, необхідна кількість станів - 20.
У такому розумінні є ще більш економічна позиційна система числення - трійкова.
Так, для запису цілих чисел від 1 до 999999999 у десятковій системі числення потрібно 90 станів, у двійковій - 60 (99999999910 = 1110111001101011001001111111112), у трійковій системі числення - 57 станів (99999999910 = 21202002000210100003).
Розглянемо практичний приклад на застосування трійкової системи числення.
Усі 5-літерні слова, складені з анлійських букв A, B, C, записані в алфавітному порядку. Початок списку наведений нижче:
1. AAAAA
2. AAAAB
3. AAAAC
4. AAABA
…Спробуємо знайти слово, яке розташоване на 150-му місці від початку списку.
Ця задача, як не дивно, пов’язана з позиційними системами числення. В словах використовується набір із трьох різних символів, для яких вказаний алфавітний порядок. Замінивши букви A, B, C відповідно на цифри 0, 1 і 2, напишемо початок списку:
1. 00000
2. 00001
3. 00002
4. 00010
…Ці числа записані в трійковій системі числення в порядку зростання.
Не важко зрозуміти, що на 150-му місці в цьому списку розташовується десяткове число 149, записане в трійковій системі числення. Тепер залишається перетворити десяткове число 149 у трійкове.
Визначимо правило перетворення чисел з десяткової системи числення в систему числення з основою q.
Для перетворення із десяткової системи числення у систему з основою q, необхідно ділити число націло на q, відкидати залишок на кожному кроці, доки не отримаємо 0, а потім записати знайдені залишки у зворотному порядку.
|
Переведемо число 149 у трійкове діленням числа націло на основу трійкової системи (3):

14910 у трійковеЗамінивши цифри
14910 = 121123на букви, отримаємо відповідь:
…
150. BCBBC
…Бінарні числа
| У цьому розіділ розглядається двійкова система числення, яка отримала широке розповсюдження у світі обчислювальних пристроїв.. |
Сьогодні будь-яку інформацію (числову, текстову, графічну, звукову та ін.) в комп’ютері можна подати за допомогою чисел.
| Переклад інформації, поданої повідомленням в якомусь первинному алфавіті, у послідовність інших символів (кодів) можна визначити як кодування інформації. |
Якщо зіставити числа з літерами, можна записувати текст у цифровій формі.
Кольори є комбінацією інтенсивності світлових потоків червоного, синього і зеленого - цю інтенсивність можна також задати в числових значеннях. Зображення легко уявити у вигляді мозаїки з кольорових квадратів, так що вони теж можуть бути представлені через числа.
Тобто, будь-які дані - це так чи інакше закодована інформація.
Для зберігання інформації комп’ютер використовує пам’ять.
Пам’ять комп’ютера поділена на багато комірок, які називаються байтами. Кожна з комірок зберігає невеликий обсяг даних і має числову адресу.
Одного байта пам’яті вистачає лише для зберігання букви або невеликого числа. Для зберігання значних обсягів даних використовують мільярди байтів пам’яті.
Кожен байт поділений на вісім менших елементів, які називаються бітами.
Термін bit (від англ. binary digit) означає двійкова цифра.
|
Біти можна уявити у вигляді «кнопок-перемикачів», які можуть бути або «увімкненими» або «вимкненими».
У комп’ютерній техніці біти є електричними компонентами, які можуть мати електричний заряд, або ні. Наявність заряду можна ототожнити з перемикачем у ввімкненому положенні, а відсутність заряду - перемикачем у вимкненому положенні.
Тобто, байт пам’яті можна представити як набір перемикачів, кожен з яких переміщений або у положення ввімкнення (ON), або вимкнення (OFF). Наприклад, якщо в байті необхідно зберегти число 81, то перемикачі будуть розміщені у таких положеннях:
Для збереження у байті англійської літери M положення перемикачів будуть наступними:
Залежно від того, чи «ввімкнено» чи «вимкнено» біт, він може мати одне з двох різних значень:
-
0(якщо біт «вимкнено»); -
1(якщо біт «увімкнено»).
Така система числення, яка складається з двох символів (у даному випадку 0 і 1), називається двійковою або бінарною.
| Будь-яка інформація, з якою працює сучасна обчислювальна техніка, в пам’яті комп’ютера представляється у вигляді чисел в двійковій системі числення. |
Числа, представлені в двійковій системі числення, ще називають двійковими або бінарними числами.
Ось приклад числа, написаного в двійковій системі числення
01110011| Якщо необхідно вказати основу системи числення, в якій записане число, то вона прописується нижнім індексом для числа. |
В нашому випадку, запис числа у двійковій системі числення буде наступним:
011100112Позиція кожної цифри 0 або 1 (розряд) у бінарному числі має своє власне значення. А саме, якщо переміщуватись ліворуч, починаючи від крайньої правої цифри, значення кожної позиції записують наступним чином (2 - основа двійкової системи числення):

Відповідно, якщо виконати обчислення (піднесення до степеня), значення кожної позиції будуть такими:

Щоб визначити десяткове значення двійкового числа, необхідно додати значення позицій для всіх 1:

Сума усіх цих значень позицій становить 115.
Таким чином, значення двійкового числа 011100112 становить 11510 у десятковій системі числення, якою користується людина в повсякденному житті.
Число 115, що зберігається в байті пам’яті, можна зобразити таким чином

Коли всі біти в байті встановлені в 0 (вимкнено), то значення байту дорівнює 0. Якщо всі біти байту встановлені на 1 (увімкнено), то байт зберігає найбільше значення, яке можна зберегти в ньому.
Найбільше значення, яке можна зберегти в байті, дорівнює 255
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255Цей ліміт існує тому, що в байті є лише вісім біт.
Що робити, якщо необхідно зберегти число більше 255? Відповідь проста: використовувати більше одного байта.
Наприклад, використаємо два байти разом. Це дає нам 16 біт. Значення позицій цих 16 біт складатимуть
-
20
-
21
-
22
-
23
-
…
-
215

Як бачимо, максимальне значення, яке можна зберегти у двох байтах, становить 65535. Тобто, в двох байтах можна зберегти будь-яке число від 0 до 65535 включно. Якщо вам потрібно зберегти число більше, ніж це, то потрібно використати більше байтів.
Для прикладу, порахуємо кількість значень, які можна зберегти, якщо використовувати 6-байтну комірку пам’яті (така комірка має 48 біт)
248 = 281 474 976 710 656Сьогодні комп’ютери обробляють різні види інформації, не лише числову, але й графічну, текстову, звукову. Тому така інформація спочатку кодується за допомогою цілих чисел, які потім перетворюються в двійковий вигляд для зберігання в комп’ютері.
Зокрема, символьна інформація також кодується за допомогою двійкових кодів.
Кожна буква належить певному алфавіту, в якому символи слідують один за одним і, отже, можуть бути пронумеровані послідовними цілими числами. Кожній букві можна зіставити ціле додатне число і назвати його кодом символу. Саме цей код буде зберігатися в пам’яті комп’ютера, а при виведенні на екран або папір «перетворюватися» у відповідний йому символ.
Відповідність букв певного алфавіту з числами-кодами формує так звану таблицю кодування. Іншими словами, кожен символ конкретного алфавіту має свій числовий код відповідно до певної таблиці кодування.
Однак, алфавітів у світі дуже багато (український, англійський та ін.), тому виникає питання: «Як закодувати всі використовувані на комп’ютері алфавіти?»
У відповідності з таблицею кодування ASCII для подання одного символу виділяється 1 байт (8 біт). Набір з 8 біт може зберегти
28 = 256різних значень.
Перші 128 значень (від 0 до 127) постійні і формують так звану основну частину таблиці, куди входять десяткові цифри, букви латинського алфавіту (великі і малі), розділові знаки (крапка, кома, дужки і ін.), а також пропуск і різні службові символи (табуляція, перенесення рядка і ін.).
Значення від 128 до 255 формують додаткову частину таблиці, де прийнято кодувати символи національних алфавітів.
Наприклад, код ASCII для великої англійської літери M становить 77. Коли ви натискаєте клавішу з великою літерою M на клавіатурі комп’ютера, число 77 зберігається в пам’яті (звичайно, як бінарне число)

Оскільки національних алфавітів надзвичайно багато, то існують розширені ASCII-таблиці у різних варіантах. Це створює додаткові труднощі у відображенні символів, наприклад, при використанні одночасно різних схем кодування.
Таблиця символів Unicode знімає обмеження на кодування символів лише одним байтом. Натомість, використовується 17 просторів, кожен з яких визначає 65536 кодів і дає можливість описати максимум
17 · 216 = 1 114 112різних символів.
Unicode має декілька реалізацій, з яких найпоширенішими є: UTF (Unicode Transformation Format) - Формат Перетворення Юнікоду і UCS (Universal Character Set) - Універсальна Таблиця Символів. Число після UTF визначає кількість бітів, що виділені під один символ, а число після UCS - кількість байтів.
UTF-8 - стандарт, який став найпоширенішим для інтернаціональних кодувань, що реалізовує представлення Unicode, сумісне з 8-бітовим кодуванням тексту.
|
UTF-8 є системою кодування зі змінною довжиною кодування символів. Це означає, що UTF-8 для кодування символів використовує від 1 до 4 байт на символ. Так, перший байт UTF-8 можна використовувати для кодування ASCII, що дає повну сумісність з кодами ASCII.
Простіше кажучи, текст, що складається тільки з символів з номером менше 128 (символи латинського алфавіту, розділові знаки і керуючі символи), при записі в UTF-8 перетворюється на звичайний текст ASCII. І навпаки, в тексті UTF-8 будь-який байт із значенням менше 128 зображає символ ASCII з тим же кодом. Решта символів Unicode зображається послідовностями завдовжки від 2 до 4 байтів.
Кодування UTF-8 дозволяє працювати в стандартизованому міжнародно прийнятому багатомовному середовищі, з порівняно незначним збільшенням обсягу даних при кодуванні.
У підсумку, для кращого розуміння про бінарні числа перегляньте відео (англ., укр. субтитри ), в якому José Américo N L F de Freitas чітко пояснює як працює бінарний код.
Перетворення додатних цілих чисел
Візьмемо, для прикладу, число 4321. У різних системах числення це число записується по-різному.

Давайте практично з’ясуємо, як перетворювати цілі числа з однієї системи числення в іншу.
Двійкове число
у 3-й системі числення
Розглянемо дванадцятизначне двійкове число і його трійковий еквівалент
Двійкове число Трійковий еквівалент
101111010101 11011012Спочатку переведемо двійкове число у його десятковий еквівалент ось так
1011110101012 = 1 · 211 + 0 · 210 + 1 · 29 + 1 · 28 + 1 · 27 + 1 · 26 + 0 · 25 + 1 · 24 + 0 · 23 + 1 · 22 + 0 · 21 + 1 · 20 = 2048 + 0 + 512 + 256 + 128 + 64 + 0 + 16 + 0 + 4 + 0 + 1 = 302910Отримали десяткове число: 302910.
Переведемо число 302910 у трійкове діленням числа націло на основу трійкової системи (3)

302910 у трійковеОтримали трійкове число: 302910 = 110110123.
Остаточний результат: 1011110101012 = 110110123.
у 8-й системі числення
Розглянемо наступне дванадцятизначне двійкове число і його вісімковий еквівалент
Двійкове число Вісімковий еквівалент
100111010001 4721Спочатку переведемо двійкове число у його десятковий еквівалент ось так
1001110100012 = 1 · 211 + 0 · 210 + 0 · 29 + 1 · 28 + 1 · 27 + 1 · 26 + 0 · 25 + 1 · 24 + 0 · 23 + 0 · 22 + 0 · 21 + 1 · 20 = 2048 + 0 + 0 + 256 + 128 + 64 + 0 + 16 + 0 + 0 + 0 + 1 = 251310Отримали десяткове число: 251310.
Переведемо число 251310 у вісімкове діленням числа націло на основу вісімкової системи (8)

251310 у вісімковеОтримали вісімкове число: 251310 = 47218.
Остаточний результат: 1001110100012 = 47218.
Двійкове число легко перетворити у вісімкове, розділивши двійкове число на групи по три біта в кожній і потім записати під цими групами відповідні цифри вісімкового еквівалента у такий спосіб
100 111 010 001
4 7 2 1у 10-й системі числення
| Для перетворення числа з будь-якої системи в десяткову необхідно помножити кожну цифру числа на десятковий еквівалент її позиційного значення і всі результати підсумувати. |
Для прикладу, поглянемо, як двійкове число 11010112 перетворюється у десяткове 10710.
Позиційне значення |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
Символьне значення |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
Множення |
1 * 64 = 64 |
1 * 32 = 32 |
0 * 16 = 0 |
1 * 8 = 8 |
0 * 4 = 0 |
1 * 2 = 2 |
1 * 1 = 1 |
Сума |
= 64 + 32 + 0 + 8 + 0 + 2 + 1 = 10710 |
||||||
11010112 = 1 · 26 + 1 · 25 + 0 · 24 + 1 · 23 + 0 · 22 + 1 · 21 + 1 · 20 = 64 + 32 + 0 + 8 + 0 + 2 + 1 = 10710у 16-й системі числення
Розглянемо наступне дванадцятизначне двійкове число і його шістнадцятковий еквівалент
Двійкове число Шістнадцятковий еквівалент
100111010001 9D1Спочатку переведемо двійкове число у його десятковий еквівалент ось так
1001110100012 = 1 · 211 + 0 · 210 + 0 · 29 + 1 · 28 + 1 · 27 + 1 · 26 + 0 · 25 + 1 · 24 + 0 · 23 + 0 · 22 + 0 · 21 + 1 · 20 = 2048 + 0 + 0 + 256 + 128 + 64 + 0 + 16 + 0 + 0 + 0 + 1 = 251310Отримали десяткове число: 251310.
Переведемо число 251310 у шістнадцяткове діленням числа націло на основу шістнадцяткової системи (16)

251310 у шістнадцятковеОтримали шістнадцяткове число: 251310 = 9D116.
Остаточний результат: 1001110100012 = 9D116.
Прослідковується закономірність перетворення числа з двійкової системи в шістнадцяткову. А саме, необхідно розділити двійкове число на групи по чотири біта в кожній і потім записати під цими групами відповідні цифри шістнадцяткового еквівалента, як це зроблено нижче
1001 1101 0001
9 D 1Трійкове число
у 2-й системі числення
Переведемо трійкове число 12123 у його десятковий еквівалент ось так
12123 = 1 · 33 + 2 · 32 + 1 · 31 + 2 · 30 = 27 + 18 + 3 + 2 = 5010Отримали десяткове число: 5010.
Переведемо число 5010 у двійкове діленням числа націло на основу двійкової системи (2)

5010 у двійковеОтримали двійкове число: 5010 = 1100102.
Остаточний результат: 12123 = 1100102.
у 8-й системі числення
Переведемо трійкове число 1212123 у його десятковий еквівалент ось так
1212123 = 1 · 35 + 2 · 34 + 1 · 33 + 2 · 32 + 1 · 31 + 2 · 30 = 243 + 162 + 27 + 18 + 3 + 2 = 45510Отримали десяткове число: 45510.
Переведемо число 45510 у вісімкове діленням числа націло на основу вісімкової системи (8)

45510 у вісімковеОтримали вісімкове число: 45510 = 7078.
Остаточний результат: 1212123 = 7078.
у 10-й системі числення
| Для перетворення числа з будь-якої системи в десяткову необхідно помножити кожну цифру числа на десятковий еквівалент її позиційного значення і всі результати підсумувати. |
Для прикладу, поглянемо, як трійкове число 1203 перетворюється у десяткове 1510.
Позиційне значення |
9 |
3 |
1 |
Символьне значення |
1 |
2 |
0 |
Множення |
1 * 9 = 9 |
2 * 3 = 6 |
0 * 1 = 0 |
Сума |
= 9 + 6 + 0 = 1510 |
||
1203 = 1 · 32 + 2 · 31 + 0 · 30 = 9 + 6 + 0 = 1510Остаточний результат: 1203 = 1510.
у 16-й системі числення
Переведемо трійкове число 20213 у шістнадцяткову систему числення. Спочатку перетворимо число у його десятковий еквівалент ось так
20213 = 2 · 33 + 0 · 32 + 2 · 31 + 1 · 30 = 54 + 0 + 6 + 1 = 6110Отримали десяткове число: 6110.
Переведемо число 6110 у шістнадцяткове діленням числа націло на основу шістнадцяткової системи (16)

6110 у шістнадцятковеОтримали шістнадцяткове число: 6110 = 3D16.
Остаточний результат: 20213 = 3D16.
Вісімкове число
у 2-й системі числення
Наприклад, є число 7258 у вісімковій системі числення і необхідно перевести його у двійкову.
Переведемо число спочатку в десяткову ось так
7258 = 7 · 82 + 2 · 81 + 5 · 80 = 448 + 16 + 5 = 46910Отримали десяткове число: 46910.
Переведемо число 46910 у двійкову систему числення діленням числа націло на основу двійкової системи (2)

46910 у двійковеОтримали двійкове число: 46910 = 1110101012.
Остаточний результат: 7258 = 1110101012.
Вісімкове число 725 також перекладається у двійкове шляхом простого запису 7 як його тризначного двійкового еквівалента 111, 2 - як 3-значного двійкового еквівалента 010, 5 - як 101, так що в цілому число записується у вигляді 9-значного двійкового числа 111010101
111 010 101
7 2 5у 3-й системі числення
Наприклад, є число 1578 у вісімковій системі числення і необхідно перевести його у трійкову.
Переведемо число спочатку в десяткову ось так
1578 = 1 · 82 + 5 · 81 + 7 · 80 = 64 + 40 + 7 = 11110Отримали десяткове число: 11110.
Переведемо число 11110 у трійкову систему числення діленням числа націло на снову трійкової системи (3)

11110 у трійковеОтримали трійкове число: 11110 = 110103.
Остаточний результат: 1578 = 110103.
у 10-й системі числення
Для прикладу, перетворимо вісімкове число 73218 у десяткове 379310.
Позиційне значення |
512 |
64 |
8 |
1 |
Символьне значення |
7 |
3 |
2 |
1 |
Множення |
7 * 512 = 3584 |
3 * 64 = 192 |
2 * 8 = 16 |
1 * 1 = 1 |
Сума |
= 3584 + 192 + 16 + 1 = 379310 |
|||
73218 = 7 · 83 + 3 · 82 + 2 · 81 + 1 · 80 = 3584 + 192 + 16 + 1 = 379310у 16-й системі числення
Наприклад, число 7258 у вісімковій системі числення необхідно перевести у шістнадцяткову. Для цього переведемо його спочатку в десяткову ось так
7258 = 7 · 82 + 2 · 81 + 5 · 80 = 448 + 16 + 5 = 46910Далі, переведемо 46910 в шістнадцяткову діленням числа націло на основу шістнадцяткової системи (16)

46910 у шістнадцятковеОстаточний результат: 7258 = 1D516.
Десяткове число
у 2-й системі числення
Переведемо число 4510 у двійкове діленням числа націло на основу двійкової системи (2)
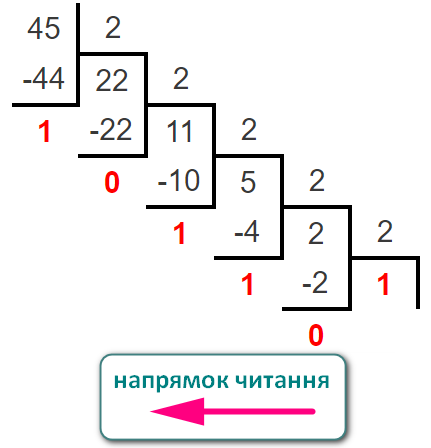
4510 у двійковеОстаточний результат: 4510 = 1011012.
у 3-й системі числення
Переведемо число 4510 у трійкове діленням числа націло на основу трійкової системи (3)

4510 у трійковеОстаточний результат: 4510 = 12003.
у 8-й системі числення
Переведемо число 4510 у вісімкове діленням числа націло на основу вісімкової системи (8)

4510 у вісімковеОстаточний результат: 4510 = 558.
у 16-й системі числення
Переведемо число 4510 у шістнадцякове діленням числа націло на основу шістнадцяткової системи (16)

4510 у шістнадцятковеОстаточний результат: 4510 = 2D16.
Шістнадцяткове число
у 2-й системі числення
Наприклад, число F3A16 у шістнадцятковій системі числення необхідно перевести у двійкову.
Для цього переведемо його спочатку в десяткову ось так
F3A16 = 15 · 162 + 3 · 161 + 10 · 160 = 3840 + 48 + 10 = 389810Переведемо 389810 у двійкову систему діленням числа націло на снову двійкової системи (2):

389810 у двійковеОтримали двійкове число: 389810 = 1111001110102.
Остаточний результат: F3A16 = 1111001110102.
Шістнадцяткове число F3A також перетворюється в двійкове за допомогою запису F як 4-значного двійкового еквівалента 1111, числа 3 як двійкового 0011, числа A як 1010, що дає 12-значне число 111100111010
1111 0011 1010
F 3 Aу 3-й системі числення
Перетворимо число FA16 у шістнадцятковій системі числення у трійкову. Для цього переведемо його спочатку в десяткову ось так
FA16 = 15 · 161 + 10 · 160 = 240 + 10 = 25010Переведемо 25010 у трійкову систему діленням числа націло на снову трійкової системи (3):
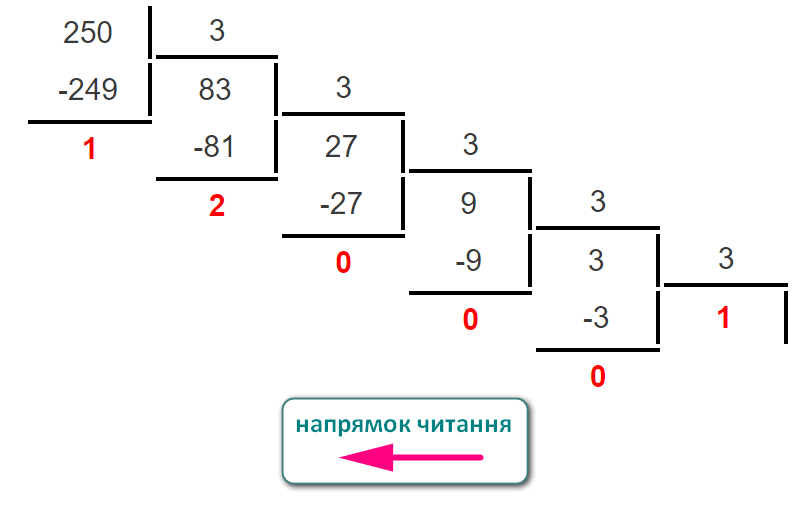
25010 у трійковеОтримали трійкове число: 25010 = 1000213.
Остаточний результат: FA16 = 1000213.
у 8-й системі числення
Наприклад, число F3A16 у шістнадцятковій системі числення необхідно перевести у вісімкову.
Для цього переведемо його спочатку в десяткову ось так
F3A16 = 15 · 162 + 3 · 161 + 10 · 160 = 3840 + 48 + 10 = 389810Переведемо 389810 у вісімкову систему діленням числа націло на снову вісімкової системи (8)

389810 у вісімковеОстаточний результат: F3A16 = 74728.
у 10-й системі числення
Для прикладу, число CD3B16 перетворюється у десяткове 5253910.
Позиційне значення |
4096 |
256 |
16 |
1 |
Символьне значення |
C |
D |
3 |
B |
Множення |
C * 4096 = 49152 |
D * 256 = 3328 |
3 * 16 = 48 |
B * 1 = 11 |
Сума |
= 49152 + 3328 + 48 + 11 = 5253910 |
|||
CD3B16 = 12 · 163 + 13 · 162 + 3 · 161 + 11 · 160 = 49152 + 3328 + 48 + 11 = 5253910Конвертер систем числення на Python
Про створення і представлення цілих чисел і чисел з рухомою крапкою у мові програмування Python читайте в Додаток B. Числа в Python.
|
Для перетворень між основними системами числення можна також використовувати застосунок Конвертер систем числення Римська-2-3-8-10-16.
Застосунок написаний на мові Python з використанням графічної бібліотеки інтерфейсів tkinter . Для користувачів Windows та Linux.
|
|
Файл-архів захищений паролем, який можна отримати, написавши на електронну адресу |
Вимоги до використання
Встановлений інтерпретатор Python версії 3.6+.
Запуск застосунку
Для запуску застосунку виконайте такі кроки:
-
Відкрити вікно термінала (Ctrl+Alt+T для
Linux; Win+R,cmdдляWindows). -
Перейти в терміналі у каталог/папку з розархівованим застосунком.
-
Виконати команду
python numeralconverter.py.
Використання застосунку
Скриншот

Відео
Основні можливості застосунку можна переглянути у відео.
Перетворення додатних дробових чисел
| Цілу і дробову частини, у записі дробового числа, завичай, розділяють символом «коми». Далі, в записі дробових чисел, будемо дотримуватися такого позначення, пам’ятаючи, що в комп’ютерних системах для цих речей використовується розділювач «крапка». |
| Якщо необхідно перевести в деяку систему числення дробове число, в якому присутня і ціла, і дробова частини, ці частини перетворюють окремо, а потім об’єднують. В результуючому записі ціла частина відділяється від дробової «комою» («крапкою»). |
Десятковий дріб
Для початку, наведемо алгоритм перетворення десяткового дробового числа в систему числення з основою q:
-
Помножити вхідне число на основу системи числення
q, в яку відбувається перетворення. Отримана, в результаті множення, ціла частина є першою цифрою після крапки в шуканому числі. -
Якщо дробова частина після множення не дорівнює
0, помножити її наq, потім цілу частину отриманого числа замінити на цифру в системіqі дописати її праворуч до результату. -
Виконати пункт 2 до тих пір, доки дробова частина не стане дорівнювати нулю або дробова частина виявиться рівною вже раніше обчисленій дробовій частині.
у 2-й системі числення
Застосуємо поданий алгоритм для перетворення десяткового дробового числа 0,187510 у двійкову систему числення і заповнимо таблицю:
| Обчислення | Ціла частина | Дробова частина |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
Обчислення (множення на основу системи числення, в яку перетворюють вхідне число) закінчуються, коли дробова частина результату (третій стовпчик таблиці) дорівнює нулю.
Ціла частина числа вже у двійковій системі числення залишається такою ж самою (0,), як і у десятковій системі, а дробова частина числа вже у двійковій системі числення буде складатися з цілих частин (другий стовпчик таблиці) в порядку виконання обчислень:
0,187510 = 0,00112
При перетворенні скінченних дробів у деяку систему числення q можна отримати скінченний дріб в системі q або нескінченний періодичний дріб. В другому випадку, зазвичай, вказують кількість значущих цифр (наближення) і округлюють число відповідним чином.
|
Тепер розглянемо, як зберігаються в пам’яті комп’ютера десяткове дробове число 0,3, записавши його в двійковій системі числення.
| Обчислення | Ціла частина | Дробова частина |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дробова частина останнього добутку дорівнює дробовій частині, яка вже була обчислена раніше (0,6), як наслідок, усі наступні цифри після першої появи цього дробового значення утворюють період дробового числа:
0,310 = 0,0(1001)2Це означає, що для зберігання десяткового числа 0,3 в двійковій системі числення необхідно нескінченне число розрядів. Оскільки реальний комп’ютер не може мати нескінченну пам’ять, то число 0,3 в двійковому вигляді зберігається в пам’яті з певним наближенням.
у будь-якій системі числення
Розглянемо ще кілька прикладів. Перетворимо десяткове дробове число 0,187510 в інші системи числення.
| Обчислення | Ціла частина | Дробова частина |
|---|---|---|
|
|
|
|
|
|
Результат:
0,187510 = 0,148| Обчислення | Ціла частина | Дробова частина |
|---|---|---|
|
|
|
Результат:
0,187510 = 0,316Переведемо десяткове дробове число 0,235610 в систему числення з основою 5.
| Обчислення | Ціла частина | Дробова частина |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дробова частина останнього добутку дорівнює дробовій частині, яка вже була обчислена раніше (0,25), як наслідок, усі наступні цифри після першої появи цього дробового значення утворюють період дробового числа:
0,235610 = 0,10421111111…5 = 0,1042(1)5Виконаємо ще одне перетворення, на цей раз дробового числа, що містить як дробову, так і цілу частини, з десяткової системи числення в інші системи.
Візьмемо десяткове дробове число 78,52310 і перетворимо його у вісімкову систему числення, залишивши чотири знаки в дробовій частині нового числа, і у шістнадцяткову - залишивши три знаки в дробовій частині нового числа.
Запишемо вхідне число як суму двох частин - цілої і дробової
78,52310 = 7810 + 0,52310і виконаємо перетворення для кожної з них.
Для перетворення цілої частини числа 78,52310 у вісімкову систему числення, поділимо цілу частину числа на основу вісімкової системи

78,52310 у вісімкову систему численняВ результаті отримаємо значення
7810 = 1168Виконаємо перетворення дробової частини числа 78,52310 у вісімкову систему числення.
| Обчислення | Ціла частина | Дробова частина |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
... |
... |
В результаті обчислень, значення дробової частини нового числа у вісімковій системі числення буде таким:
0,52310 = 0,413615…8Врахувавши умову, за якою необхідно залишити чотири знаки в дробовій частині нового числа, отримаємо:
0,52310 = 0,41368Склавши цілу і дробову частину, запишемо значення десяткового дробового числа 78,52310 у 8-ій системі числення:
78,52310 = 116,41368Для перетворення цілої частини числа 78,52310 у шістнадцяткову систему числення, поділимо цілу частину числа на основу шістнадцяткової системи

78,52310 у шістнадцяткову систему численняВ результаті отримаємо значення
7810 = 4E16Виконаємо перетворення дробової частини числа 78,52310 у шістнадцяткову систему числення.
| Обчислення | Ціла частина | Дробова частина |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
... |
... |
В результаті обчислень, значення дробової частини нового числа у шістнадцятковій системі числення буде таким:
0,52310 = 0,85E353F7…16Врахувавши умову, за якою необхідно залишити три знаки в дробовій частині нового числа, отримаємо:
0,52310 = 0,85E16Склавши цілу і дробову частину, запишемо значення десяткового дробового числа 78,52310 у 16-ій системі числення:
78,52310 = 4E,85E16Двійковий дріб
у 10-й системі числення
Запишемо значення скінченного двійкового дробу 0,110112 в десятковій системі числення. Для цього скористаємось розгорнутою формою запису числа:
0,110112 = 0 · 20 + 1 · 2-1 + 1 · 2-2 + 0 · 2-3 + 1 · 2-4 + 1 · 2-5 = 0 + 0,5 + 0,25 + 0 + 0,0625 + 0,03125 = 0,8437510у будь-якій системі числення
Щоб перетворити двійкове дробове число в систему з основою q (окрім десяткової), необхідно спочатку перетворити двійкове число в десяткову систему, а потім вже десяткове число перетворити в систему q. Зробимо це.
Візьмемо двійкове дробове число 0,01012 і перетворимо, наприклад, в шістнадцяткову систему числення. Отже, спочатку перетворимо число 0,01012 в десяткову систему, використовуючи розгорнуту форму запису числа:
0,01012 = 0 · 20 + 0 · 2-1 + 1 · 2-2 + 0 · 2-3 + 1 · 2-4 = 0 + 0 + 0,25 + 0 + 0,0625 = 0,312510Далі, ціла частина нового числа буде дорівнювати 016, а дробову частину нового числа знаходимо множенням дробової частини двійкового дробового числа на основу 16:
| Обчислення | Ціла частина | Дробова частина |
|---|---|---|
|
|
|
Отже, в результаті:
0,312510 = 0,516Додаючи цілу і дробову частини, отримуємо потрібне значення в шістнадцятковій системі:
016 + 0,516 = 0,516Спробуємо перетворити двійкові дробові числа в інші системи числення, використовуючи інший спосіб, що описується наступним алгоритмом.
Щоб записати дробове двійкове число в системі числення q, необхідно:
-
Цілу і дробову частини двійкового числа, починаючи з крапки (коми), розбити на групи по
nцифр в кожній. -
Якщо в останніх правої і лівої групах буде менше
nрозрядів, то необхідно доповнити, відповідно, справа і зліва нулями до потрібного числа розрядів. -
Розглянути кожну з груп як
n-розрядне двійкове число і записати його відповідною цифрою в системі числення з основоюq.
Наприклад, перетворимо число 1011101,101112 в шістнадцяткову систему числення.
Розіб’ємо цілу і дробову частини числа по чотири групи двійкових цифр вліво і вправо від коми відповідно, записавши нулі там, де знаків менше чотирьох (для цілої частини додаємо нулі зліва, для дробової частини додаємо нулі справа):
0101 1101, 1011 1000Використаємо шістнадцятково-двійкову таблицю, в якій зберігаються шістнадцяткові цифри та їхні двійкові еквіваленти, окрім того, усі двійкові числа записані в чотирьохзначному вигляді (там, де знаків менше чотирьох, зліва додані нулі):
| 16 | 2 | 16 | 2 |
|---|---|---|---|
0 |
0000 |
8 |
1000 |
1 |
0001 |
9 |
1001 |
2 |
0010 |
A |
1010 |
3 |
0011 |
B |
1011 |
4 |
0100 |
C |
1100 |
5 |
0101 |
D |
1101 |
6 |
0110 |
E |
1110 |
7 |
0111 |
F |
1111 |
В результаті
1011101,101112 = 5D,B816Аналогічно використаємо вісімково-двійкову таблицю для перетворення числа 1011101,101112 у вісімкову систему числення. У цій таблиці кожній вісімковій цифрі відповідає трійка двійкових цифр.
| 8 | 2 |
|---|---|
0 |
000 |
1 |
001 |
2 |
010 |
3 |
011 |
4 |
100 |
5 |
101 |
6 |
110 |
7 |
111 |
Розіб’ємо число по три двійкових знаки від коми вліво і вправо відповідно (там, де знаків менше трьох, для цілої частини додаємо нулі зліва, для дробової частини додаємо нулі справа).
001 011 101, 101 110В результаті
1011101,101112 = 135,568Дріб у будь-якій системі числення
у 10-й системі числення
Продемонструємо, як можна перетворити скінченне дробове число, записане в деякій системі числення з основою q в десяткову систему числення.
Перетворимо дробове скінченне число 0,E16 в десяткову систему числення. Для цього використаємо розгорнуту форму запису числа:
0,E16 = 0 · 160 + 14 · 16-1 = 0 + 0,875 = 0,87510Таблиця переведення дробових чисел
| Для демонстрації процесу переведення додатних дробових чисел з однієї системи числення у іншу можна використати таблицю переведення Дробові числа. В окремому випадку, таблицю можна також використовувати для переведення з однієї системи числення у іншу додатних цілих чисел. |
| При використанні електронної таблиці Дробові числа, результати перетворень (обчислень) для різної точності (кількість значущих цифр у числі) можуть відрізнятися. |
Використання онлайн-сервісів
Для перетворень між різними системами числення можна використовувати різні онлайн-калькулятори, на зразок таких:
Задачі для самостійного виконання
Непозиційні системи числення
-
Яке найбільше число можна записати в класичній Римській системі числення?
-
Які десяткові числа записані за допомогою римських цифр:
MMMD,MCCVII,MCMXCVIII? -
Перетворіть в римську систему десяткові числа:
15,234,1999,2666,3888. -
Перетворіть в десяткову систему римські числа:
MMMCXI,MCMXCIX,MCXCVII,MMDCCCLXXXIX. -
Яку значення позначає цифра
8в десяткових числах3538,8126,81і891? -
Що можна сказати про числа
111іIII?
Позиційні системи числення і основні поняття систем числення
-
Запишіть алфавіти для таких систем числення:
5,7,11. -
Яке найменше значення основи повинно бути у системах числення, щоб в них існували числа:
123,145,112і567? -
Яке найменше значення основи повинно бути у системах числення, щоб в них існували числа:
22,896,1100іA007? -
Запишіть в розгорнутій формі числа:
115,2310,0,4568,E4B,1216. -
Запишіть за допомогою схеми Горнера числа:
2644110,44558,92D16. -
Знайдіть всі основи систем числення, в яких запис числа
39закінчується на6. -
В системі числення з деякою основою
xдесяткове число55записується у вигляді1004x. Яка основа системи числення? -
Запис числа
55в системі числення з деякою основоюxвиглядає так:212x. Вкажіть основу системи числення. -
Знайдіть всі основи систем числення, в яких запис числа
30закінчується на8. -
Знайдіть найменшу основу системи числення, в якій запис числа
30є тризначним. -
Знайдіть усі десяткові числа, які не більші
25, запис яких в системі числення з основою5закінчується на3. -
Знайдіть усі десяткові числа, які не більші
30, запис яких в системі числення з основою6починається на4. -
Знайдіть усі десяткові числа, які не більші
25, запис яких в системі числення з основою8закінчується на6. -
Знайдіть усі десяткові числа, які не більші
30, запис яких в системі числення з основою7починається на5. -
Всі 5-літерні слова, складені з букв
A,M,R,S, записані в алфавітному порядку у список:
1. AAAAA
2. AAAAM
3. AAAAR
4. AAAAS
…-
визначте, скільки всього слів у списку;
-
вкажіть слова, які розташовані на
150-му,250-му,350-му і450-му місці; -
вкажіть порядкові номери слів:
MARS,SARM,ARSM; -
вкажіть номери першого і останнього слів, які починаються з літери
M.
Бінарні числа
-
Які символи таблиці
ASCIIмають коди50і81? -
Скільки бітів пам’яті комп’ютера займає словосполучення
computer scienceв 16-бітномму кодуванняUnicode? -
Яке слово зашифровано послідовністю десяткових кодів
116 101 97 99 104 101 114в кодуванніASCII? -
За допомогою послідовності десяткових кодів зашифровано слова
computer. Яка послідовність десяткових кодів відповідатиме цьому ж слову, записаному великими літерами? -
За шістнадцятковим кодом
50 79 74 68 6F 6Eвідновіть десятковий код і, користуючись таблицею кодування символів, розшифруйте слово. -
Довжина двійкового коду тексту, набраного на комп’ютері з використанням кодування
Unicode-4кБ. Визначте кількість символів у тексті. -
Автоматичний пристрій здійснив перекодування інформаційного повідомлення українською мовою, спочатку записаного в
16-бітному кодіUnicode, у8-бітне кодуванняWindows-1251, при цьому довжина двійкового коду повідомлення становила60байт. Визначте довжину двійкового коду повідомлення до перекодування. -
Яке мінімальне число біт на символ потрібно виділити в пам’яті, якщо необхідно використовувати не менше
10символів одночасно? -
Скільки різних символів можна використовувати за умови, що на кожний символ відводиться
9біт? -
При перекодуванні повідомлення українською мовою із
16-бітного кодуUnicodeв8-бітне кодуванняKOI8-U, воно зменшилось на560бітів. Яка довжина повідомлення у символах? -
При перекодуванні повідомлення із
8-бітного коду в16-бітне кодуванняUnicode, його об’єм збільшився на2048байтів. Який інформаційний об’єм повідомлення до перекодування (у байтах)? -
Визначте, не використовуючи таблицю кодування
ASCII, десятковийASCII-код символуy, якщо відомі наступні коди:A - 65,Y - 89,a - 97. -
Оцініть інформаційний об’єм (в кілобайтах) тексту, що складається із
40сторінок, якщо на кожній сторінці розміщується в середньому32рядки по60символів в рядку (включаючи пропуски). Текст закодований у8-бітному кодуванні.
Перетворення чисел
-
Виберіть найбільше число:
102,108,1010,1012,1016,1022. -
Запишіть в десятковій системі числення числа:
3338,3339,33316. -
Перетворіть шістнадцяткове число
AEв двійкове. -
Перетворіть вісімкове число
7241в двійкове. -
Перетворіть шістнадцяткове число
2FBCв вісімкове. -
Перетворіть двійкове число
1001111в десяткове. -
Перетворіть вісімкове число
503в десяткове. -
Перетворіть шістнадцяткове число
EFD2в десяткове. -
Перетворіть десяткове число
123в двійкове, вісімкове і шістнадцяткове. -
Перетворіть десяткові числа
37і315у вісімкові і шістнадцяткові. -
Вкажіть двійкове подання десяткового числа
345. -
Перетворіть числа
101111001,10101010,1000001у вісімкову, десяткову і шістнадцяткову системи числення. -
Перетворіть двійкове число
110101011010у вісімкове і шістнадцяткове представлення. -
Перетворіть числа:
2416в двійкове,AC616у вісімкове,F1616у десяткове. -
Перетворіть числа:
101001012в десяткове,168в двійкове,202110в шістнадцяткове. -
Перевести цілі числа із десяткової системи числення в двійкову систему:
24,124,243,5243. -
Перевести цілі числа із десяткової системи числення у вісімкову систему:
519,312,58,742. -
Перевести цілі двійкові числа у вісімкову систему:
1100001101011,101,10000000001,101011. -
Перевести цілі двійкові числа у шістнадцяткову систему:
1100101,10111,1010101,11111111. -
Перевести цілі вісімкові числа у двійкову систему:
256,171,652. -
Перевести цілі шістнадцяткові числа у двійкову систему:
1AC5,FFAA,BC5. -
Перевести цілі шістнадцяткові числа у вісімкову систему:
A25,84B,D125. -
Перевести цілі вісімкові числа у шістнадцяткову систему:
352,772,665. -
В яких системах числення справедливі такі рівності:
2 · 2 = 10,2 · 3 = 11,3 · 3 = 13? -
Скільки разів зустрічається цифра
3в записі числел21,22,23, ...,30,31в системі числення з основою7? -
В системі числення з деякою основою
xчисло12записується у вигляді110x. Яка основа системи числення? -
Яке число слідує за числом
11414у14системі числення? -
Яке число знаходиться перед числом
1018у18системі числення? -
Яке з чисел більше:
510чи105,10002чи108? -
Запишіть в десятковій системі числення числа:
34,15,2213,1157,ABC16. -
В яких системах числення
10- число непарне? -
Запишіть десяткові числа у діапазоні від
20до30включно у двійковій, вісімковій і шастнадцятковій системах числення. -
У скільки разів збільшиться число
324, якщо справа до нього дописати три нулі? -
Запишіть десяткові еквіваленти числа
101010, якщо вважати, що число записане у всіх системах числення - від двійкової до десяткової включно. -
Перетворіть десяткові дроби у двійкову систему числення:
0,655,0,6134,0,333,0,9412. В двійковому записі зберегти шість знаків. -
Перетворіть десяткові дроби у шістнадцяткову систему числення:
0,547,0,1011,0,1234,0,8899. В двійковому записі зберегти шість знаків. -
Перетворіть у вісімкову систему числення скінченне шістнадцяткове дробове число
BF3,616. -
Перетворіть десяткові дроби
0,1,0,3і0,8в трійкову і вісімкову системи числення. -
Перетворіть десяткові числа
345,0,125і45,65у12-ву систему числення. -
Перетворіть десяткові числа
675,0,345і12,13у4-ву систему числення. -
Перетворіть десяткові числа
890,0,345і1,3у7-ву систему числення. -
Перетворіть десяткові числа
625,0,625і625,75у6-ву систему числення. -
Перетворіть десяткові числа
99,0,805і508,99у8-ву систему числення. -
Перетворіть числа:
324в двійкове,15,26в десяткове,101,11012в шістнадцяткове. -
Перетворіть числа:
1A1,1E16в двійкове,111,2223в десяткове,2738в шістнадцяткове. -
Перевести вісімкові числа у двійкову систему:
0,231,345,12,67,35. -
Перевести шістнадцяткові числа у двійкову систему:
0,FDD,FDA,12F,DDFF,A. -
Перетворіть десяткові дроби у трійкову систему числення:
40,5,90,99,124,44,225,52. В трійковому записі зберегти п’ять знаків. -
Перетворіть десяткові дробові числа
12,42,112,241і25,81в систему з основою4. В записі числа зберегти три знаки. -
Перетворіть десяткові числа
11,8,15,3і22,7в двійкову систему, виділивши період в дробовій частині утворених чисел. -
Перетворіть дробові числа у вісімкову і шістнадцяткову системи числення:
100010,011101,1111000000,101,100001,111,101111,011. -
Перетворіть двійкові числа у вісімкову систему числення:
0,1101,0,111,0,01,0,11011011. -
Перетворіть двійкові числа у шістнадцяткову систему числення:
0,1001,0,011011,0,101001000,0,11111111. -
Перетворіть двійкові числа у вісімкову систему числення:
10001,1001,100,011011,11,101,101010,111. -
Перетворіть двійкові числа у шістнадцяткову систему числення:
1,101,1000,0001,111,111,110011,1001. -
Перевести шістнадцяткові числа у вісімкову систему:
24A,9F,21D,123,0,DFD4. -
Перевести вісімкові числа у шістнадцяткову систему:
0,3438,0,7645,42,75. -
Перевести число
12345,6789в27-ву систему числення. -
Перевести число
ABCD,EF16у вісімкову систему числення.
Додаток A
-
Визначити додатковий код десяткових чисел
-1,-10,-52,-100для восьмирозрядної і шістнадцятковорозрядної комірок пам’яті. -
Визначити подання десяткового цілого від’ємного числа
-1501у двійковій і шістнадцятковій формах. -
Запишіть дробові числа
0,006223,1234,4567,0,54в нормалізованй формі з рухомою крапкою в десятковій системі числення. -
Порівняйте числа:
318,478510 · 109 і 3,18478510 · 1011
218,478510 · 10-3 і 21847,8510 · 10-4
0,11012 · 22 і 1012 · 2-2-
Визначте, як зберігаються в
4-байтовій комірці пам’яті десяткові числа100,-100,-0,1,45,65, і отримайте їх шістнадцяткові коди. -
Визначте, яким десятковим числам, що зберігаються в
4-байтовій комірці пам’яті, відповідають шістнадцяткові коди:C981100016,BFC0000016,3FC0000016. -
Які з чисел
4316,1010102,12910і-13510можна зберегти в одному байті (у восьмирозрядній комірці пам’яті)?
Додаток B
-
Обчисліть і виведіть на екран:
22222-
Обчисліть
15!факторіал і виведіть результат. -
Обчисліть довжину гіпотенузи в прямокутному трикутнику зі сторонами
2021і1202. -
Число
2021записали100раз поспіль. Отримане число піднесли до квадрату. Скільки вийшло? -
Запишіть слово
Python1000разів поспіль. Надрукуйте утворений рядок. -
Використовуючи можливості мови програмування
Pythonперетворіть числа у десяткову систему числення:2268,1203,10111101011011101112,A1B216,31034,FG19,512521,40826,202934,198136. -
Використовуючи можливості мови програмування
Pythonперетворіть числа у десяткову систему числення:0o14,0b10101011010011,0xD35C,0o1234,0xA9C,0b1000110111. -
За допомогою рядкового форматування надрукуйте
56знаків після десяткової крапки для таких чисел:0,1,0,3,12,379,3,66,42,545. -
Перетворіть десяткові дробові числа в шістнадцяткову систему числення за допомогою
Python:0,1425,5,34,145,12. -
Перетворіть шістнадцяткове подання чисел з рухомою крапкою у
Pythonу десяткову систему числення:0x1,30a3d70a3d70ap+3,0x1,999999999999ap-2,'0x1,8000000000000p+0.
Словник основних понять
- Додатковий код
-
використовують для подання в комп’ютері цілих від’ємних чисел, оскільки він дозволяє замінити арфиметичну дію віднімання дією додавання, що суттєво збільшує швидкість обчислень.
- Експоненціальна форма запису числа
-
представлення дробових чисел у вигляді мантиси і порядку, зручний при представленні дуже великих і дуже малих чисел, а також для уніфікації їх написання.
- Знаковий розряд
-
розряд для зберігання знаку числа.
- Кодування інформації
-
переклад інформації, поданої повідомленням в якомусь первинному алфавіті, у послідовність інших символів (кодів).
- Комп’ютерна арифметика
-
включає алгоритми виконання операцій над числами з рухомою крапкою , дробами та дуже великими числами .
- Літерал у мові програмування
Python -
спосіб створення об’єктів. Якщо в тексті коду зустрічається літерал, то для цього літералу створюється окремий об’єкт деякого типу, тобто, генерується відповідний код, що створює об’єкт, який містить значення цього літералу. Запис, наприклад,
a = 5, можна прочитати як за допомогою числового літералу5створений цілочисельний об’єкт зі значенням5, на який посилається ім’яa. Інші приклади літералів:
3 # числовий літерал
2.48 # числовий літерал
"some text" # рядковий літерал
[3, 5, 7, 9] # літерал списку
{'a': 1, 'b': 2, 'c': 3} # літерал словника- Мантиса
-
дробова частина нормалізованого числа при використанні арифметики з рухомою крапкою.
- Натуральні числа
-
числа, що виникають природним чином при лічбі:
1,2,3, ... . Натуральні числа можна записувати за допомогою десяти цифр:0,1,2,3,4,5,6,7,8,9. - Непозиційна система числення
-
система числення, в якій значення цифри у числі не залежить від позиції цієї цифри в записі числа.
- Нескінченний періодичний десятковий дріб
-
число, яке не може бути точно виражене у вигляді десяткового дробу. Наприклад, при дробі
1/3ми одержуємо0,3333...- це нескінченний періодичний дріб з періодом3, по іншому записують як0,(3). Прикладом нескінченного неперіодичного числа є число π -3,141592.... - Нормалізована форма подання числа
-
подання числа в експоненціальній формі, де ціла частина мантиси складається із єдиної ненульової цифри. В цьому випадку, мантиса повинна задовільняти умову:
1 ≤ m < n, деm- мантиса,n- основа системи числення. - Основа системи числення
-
кількість знаків (цифр), які використовуються для запису числа.
- Переповнення
-
пов’язане з обмеженою кількістю розрядів комірки пам’яті для зберігання числа, і не пов’язане із системою числення.
- Позиційна система числення
-
система числення, в якій значення цифри залежить від позиції цифри у записі числа. В позиційних системах числення значення, яке позначене цифрою в числі, залежить від позиції цифри в записі числа, а в непозиційних - значення цифри у числі не залежить від позиції цієї цифри в записі числа.
- Прямий код
-
форма подання числа, при якій старший розряд комірки пам’яті відводиться під знак, усі інші
k-1розрядів - під цифри числа. - Розгорнута форма запису числа
-
дозволяє записувати будь-яке ціле або дробове (подається як сума цілої і дробової частин, будь-яка з цих частин може бути відсутня) невід’ємне число в заданій позиційній системі числення. Для позначення від’ємного числа використовується знак
-, після якого, за тими самими правилами, записується модуль числа. Схему Горнера і розгорнуту форму запису числа можна використовувати для перетворення числа із будь-якої системи числення в десяткову систему числення. - Розряд
-
позиція цифри у числі.
- Розрядність
-
кількість цифр, з яких складається число. Наприклад,
125- трирозрядне число,01110011- восьмирозрядне число. Розряди нумеруються справа наліво і рахунок починається з0. - Система числення
-
правила запису чисел за допомогою спеціальних знаків - цифр, а також відповідні правила виконання дій з цими числами.
- Скінченний десятковий дріб
-
число, яке може бути точно виражене у вигляді десяткового дробу. Наприклад, дріб
1/2можна представити десятковим дробом0,5. - Унарна система числення
-
цифрами такої системи можуть використовуватися будь-які однакові предмети або символи (камінці, вузлики, засічки на дереві тощо).
- Формат з фіксованою крапкою
-
представлення дробового числа, що має фіксовану кількість цифр після відокремлювальної крапки.
- Число з рухомою крапкою
-
форма представлення дробових чисел, в якій число зберігається у формі мантиси і показника степеня.
Додаток A: Зберігання чисел в пам’яті комп’ютера
Отже, як ми з’ясували, будь-яка інформація, яка обробляється сучасними комп’ютерами, представлена в двійковому вигляді.
Кожна комірка пам’яті комп’ютера є фізичною системою, що складається з деякого числа однорідних елементів, які можуть перебувати у двох станах, один з яких відповідає нулю, інший - одиниці.
Кожен такий елемент називається розрядом і використовується для запису одного із розрядів двійкового числа. Комірку із розрядами можна представити так:
|
|
|
... |
|
|
|
Для подання чисел в пам’яті комп’ютера використовуються два формати: формат з фіксованою крапкою (цілі числа) і формат з рухомою крапкою (цілі і дробові числа).
| Термін «рухома крапка» вказує на те, що немає постійної кількості цифр до або після десяткової крапки числа. Іншими словами, сама десяткова крапка може «рухатися». |
Сформулюємо кілька тез, що визначають особливості зберігання чисел в пам’яті комп’ютера.
-
Для комп’ютерного подання цілих чисел використовують різні способи, які відрізняються кількістю розрядів і наявністю чи відсутністю знакового розряду - розряду для зберігання знаку числа.
-
Беззнакове подання можна використовувати лише для додатних цілих чисел, від’ємні числа представляються лише в знаковому вигляді.
-
При беззнаковому поданні усі розряди комірки пам’яті відводяться під саме число. При поданні зі знаком, найстарший (лівий) розряд відводиться під знак числа, усі інші розряди - під саме число.
-
Якщо число додатне, то в знаковий розряд записується
0, якщо число від’ємне, то в знаковий розряд записується1. -
Двійкові розряди в комірці пам’яті нумеруються від
0доk-1справа наліво. Старший,k-1-й розряд (який низивається знаковим) у поданні будь-якого додатного числа дорівнює0, у поданні від’ємного числа - дорівнює1.
Цілі числа без знаку
Щоб отримати в комп’ютерному поданні беззнакове число в k-розрядній комірці пам’яті, необхідно перетворити це число в двійкову систему числення і доповнити результат зліва незначущими нулями до k розрядів.
|
Зрозуміло, що числа, які зберігаються в пам’яті комп’ютера, не можуь бути як завгодно великими. Вони мають деякі граничні значення, так як кількість розрядів, що відведені для зберігання числа, обмежена, і точність обчислень також є обмеженою.
В загальному випадку, якщо в системі числення з основою q для запису цілого числа використовується k розрядів, максимально допустиме число X обчислюється за формулою:
Xмаксимальне = qk-1Максимальне число складається із усіх одиниць і визначається розрядністю (кількістю бітів) k.
Кількість розрядів, k |
Максимальне число Xмаксимальне = 2k-1 |
|---|---|
|
|
|
|
|
|
|
|
Мінімальне значення для беззнакових цілих чисел завжди рівне 0 (усі розряди нульові).
Наприклад, необхідно отримати двійкове подання цілого беззнакового додатного числа 4010 у 1-байтовій комірці пам’яті. Спочатку перетворимо число 4010 у двійкове:
4010 = 1010002В 8-розрядну комірку пам’яті двійкове подання числа 4010 запишеться так (доповнимо отримане двійкове число зліва незначущими нулями, щоб кількіть розрядів стала 8):
0010 1000Якщо використовувати для зберігання числа 16-розрядну комірку пам’яті (2-байтову), то двійковий запис числа 4010 буде наступним:
0000 0000 0010 1000У таблиці нижче наведені деякі восьмирозрядні числа в десятковому, шістнадцятковому і двійковому поданнях.
|
|
|
... |
|
|
... |
|
|
|
|
... |
|
|
... |
|
|
|
|
... |
|
|
... |
|
Максимальне беззнакове додатне ціле число, яке можна зберегти у 8-розрядній комірці пам’яті, - 25510. А що відбудеться, якщо в комірці даної розрядності потрібно зберегти число 25610 або більше?
Перетворимо число 25610 в двійкову систему числення:
1 0000 00002У даному випадку, число 25610 не поміщається в даній кількості розрядів, необхідний ще один розряд, якого не має у 8-розрядній комірці пам’яті. Це називається переповненням.
| Переповнення пов’язане з обмеженою кількістю розрядів комірки пам’яті для зберігання числа, і не пов’язане із системою числення. |
Відкинувши додатковий розряд (1), в 8-розрядній комірці буде збережений 0 замість 25610. Отже:
25510 + 110 = 0Такий результат дивний, але саме так відбувається в реальному комп’ютері. При k розрядах комп’ютерна арифметика використовує ділення на
2kз остачею. Тобто, для числа 256 і при k = 8 маємо:
256 % 28 = 256 % 256 = 0
Символ % в даному випадку позначає оператор ділення з остачею.
|
Разом з тим, аналогічний результат можна отримати, коли від 0 віднімемо 110. Для цього необхідно «позичити» одиницю із умовно доданого дев’ятого розряду, що міститься за межами 8-розрядної комірки:
1 0000 00002 - 0 0000 00012 = 0 1111 11112або ж
0 - 110 = 25510| В ході роботи з мовами програмування слід враховувати можливість переповнення. |
Подивимось на прикладі, як проблема переповнення впливає на достовірність результатів. Наприклад, при зберіганні числа 27010, яке має двійкове значення
1 0000 11102в 8-розрядній комірці пам’яті, насправді, буде збережено число 1410:
270 % 28 = 270 % 256 = 1410Якщо збільшувати число далі і пробувати зберігати його в 8-розрядній комірці пам’яті, то можна дійти до якогось максимального значення і знову повернутися до мінімального. Наприклад, якщо взяти число 51210, яке у двійковій системі числення записується
10 0000 00002у 8-розрядній комірці пам’яті буде збережено число 0, що не є достовірним результатом.
Якщо уважно подивитись на отримані результати, то можна помітити, що при послідовному збільшенні значення числа на одиницю ми доходимо до максимального значенння і повертаємось до мінімального - свого роду, рухаємося циклічно по колу. Така поведінка чисел зображуються, замість традиційного відрізка математичної числової осі, за допомогою кола.
8-розрядній комірці пам’яті|
В |
Цілі числа із знаком
| Для того, щоб розрізняти додатні і від’ємні числа, у двійковому коді виділяється один біт (розряд) для збергіання знаку числа - знаковий розряд. |
Додатні числа
Максимальне додатне ціле число, яке можна записати в знаковому поданні в k розрядах, дорівнює
2k-1-1Це майже у два рази менше максимального числа в беззнаковому поданні в тих же k розрядах.
Перевіримо це на такому прикладі. Для зберігання цілих чисел в комп’ютері використовується 16-розрядна комірка (два байти). Визначимо, який діапазон чисел можна зберегти в такій комірці, якщо зберігати необхідно лише додатні цілі числа (беззнаковий варіант).
Отже, всього в k = 16-розрядній комірці може зберігатися
216 = 65536різних значень. Тому, діапазон значень буде наступним:
від 0 до 65535 (від 0 до 2k-1)Для зберігання і додатних, і від’ємних чисел зі знаком (знаковий варіант) в 16-розрядній комірці буде такий діапазон значень:
від -32768 до 32767 (від -2k-1 до 2k-1-1)Розглянемо число 4510 = 1011012 у восьмирозрядному поданні:
0010 11012Це ж число в шістнадцятирозрядному поданні буде записано так:
0000 0000 0010 11012В обох випадках, як для 1-байтової, так і 2-байтової комірок пам’яті, неважливо, знакове чи беззнакове подання числа при цьому використовується.
А для числа 24510 = 111101012 подання в одному байті (8 розрядів) із знаком є неможливим, оскільки максимально допустиме число в восьмирозрядному поданні дорівнює 127, а в беззнаковому восьмирозрядному поданні число 24510 має вигляд:
1111 01012| Очевидно, що в комірках одного і того ж розміру можна подати більший діапазон цілих додатних чисел в безнаковому вигляді, ніж чисел зі знаком. Тому, якщо відомо наперед, що деяка числова величина завжди є додатною, то вигідніше розглядати її як беззнакову. |
При знаковому поданні цілих чисел з’являється таке поняття як прямий код.
Форма подання числа, при якій старший розряд комірки пам’яті відводиться під знак, усі інші k-1 розрядів - під цифри числа, називається прямим кодом.
|
Наприклад, прямі коди для двійкових чисел
110012
-110012для 8-розрядної комірки будуть відповідно такими
0001 10012
1001 10012| Додатні цілі числа подаються в комп’ютері за допомогою прямого коду. |
Від’ємні числа
Прямий код від’ємного цілого числа відрізняється від прямого коду відповідного додатного цілого числа значенням знакового розряду.
Але замість прямого коду, для подання від’ємних цілих чисел в комп’ютері, використовується додатковий код.
Алгоритм використання додаткового коду для зберігання цілого від’ємного числа:
-
Перетворити модуль числа у прямий код в
kдвійкових розрядах. -
Отримати зворотний код вхідного числа заміною
0на1і1на0(інвертувати значення усіх розрядів). -
До отриманого зворотного коду, який трактується як
k-розрядне додатне двійкове число, додати1.
Розглянемо наступний приклад. Отримаємо подання цілого від’ємного числа -202010 для зберігання у 16-розрядній комірці пам’яті.
Перетворимо число -202010 у двійкову форму:
111111001002і запишемо прямий код для модуля вхідного числа:
0000 0111 1110 01002Далі утворимо зворотний код числа -202010
1111 1000 0001 10112і додамо одиницю для утворення додаткового коду
1111 1000 0001 11002| У підручнику не розглядаються правила виконання математичних операцій з двійковими числами. Тому, для виконання таких дій, використовуйте двійковий калькулятор . |
Додатковий код доповнює вхідне число -202010 до
2kЯкщо додати додатковий код
11111000000111002 = 6351610до вхідного числа -202010, то сума буде дорівнювати значенню 100000000000000002 = 6553610, що свідчить про переповнення (вихід за межі 16-розрядної сітки). Зважаючи на те, що перенесення із старшого розряду не враховується, сума дорівнює нулю.
Додатковий код від’ємного цілого числа - це доповнення модуля цього числа до 2 в степені k (або до нуля в k-розрядній арифметиці).
|
Побудуємо додатковий восьмирозрядний код для чисел -12810, -12710, -0 і представимо результати у таблиці.
Число |
|
|
|
Прямий код модуля числа |
|
|
|
Зворотний код |
|
|
|
Додатковий код |
|
|
|
Для числа -12810 прямий код співпадає з додатковим, а додатковий код числа -0 співпадає зі звичайним нулем. При перетворенні зворотного коду для числа -0 в його додатковий код, правила звичайної двійкової арифметики порушуються, а саме:
1111 11112 + 1 = 1 0000 00002 = 2k = 0Використаємо ще один алгоритм отримання додаткового коду від’ємного цілого числа, але який є простішим для проведення обчислень «вручну».
| Виконати інверсію усіх старших бітів (розрядів) числа, окрім останньої (молодшої) одиниці і тих нулів, які йдуть за нею. |
Застосуємо цей алгоритм для нашого прикладу - змінивши прямий код 0000 0111 1110 01002 цілого від’ємного числа -202010 за поданим алгоритмом, отримаємо той самий додатковий код, що і у попередньому випадку
1111 1000 0001 11002Проведемо зворотні дії. Отримаємо десяткове значення числа по його додатковому коду 100101112, виконавши такий алгоритм:
-
Виконати інверсію додаткового коду
100101112 = 011010002-
Додати до результату
1:
011010002 + 12 = 011010012-
Перетворити отримане двійкове значення в десяткову систему числення:
011010012 = 0 · 27 + 1 · 26 + 1 · 25 + 1 · 24 + 1 · 23 + 1 · 22 + 1 · 21 + 1 · 20 = 0 + 64 + 32 + 0 + 8 + 0 + 0 + 1 = 10510Результатом обчислень і перетворень буде число
-10510Розглянемо таблицю двійкових і шістнадцяткових кодів деяких цілих восьмирозрядних додатних і від’ємних чисел.
|
|
|
... |
|
|
|
... |
|
|
|
|
... |
|
|
|
... |
|
|
|
|
... |
|
|
|
... |
|
Аналізуючи таблицю, слід звернути увагу на стрибок при переході від -1 до 0 і граничні значення 12710 і -12810. За даними таблиці побудуємо коло для чисел зі знаком.
8-розрядній комірці пам’ятіВарто звернути увагу, що порівняння кодів більших 7F16 для чисел з урахуванням і без урахування знака дає різні результати. Наприклад, для беззнакових чисел значення 8116 (12910) точно більше за 7F16 (12710). Для чисел із знаком, навпаки, від’ємне значення 8116 (-12710) буде, безперечно, менше, ніж 7F16 (12710). Порівняння кодів цілих чисел без знаку і зі знаком наведені в таблиці нижче.
Код |
|
|
|
... |
|
|
|
... |
|
|
Без знаку |
|
|
|
... |
|
|
|
... |
|
|
Зі знаком |
|
|
|
... |
|
|
|
... |
|
|
Ще одним результатом порівняння чисел із знаком і без нього є те, що загальне число їх значень однакове, а їхні діапазони зсунуті на числовій осі.
8-розрядній комірці пам’ятіЦілі числа зі знаком, що подаються в k-розрядах, належать діапазону
[-2k-1, 2k-1-1]який не є симетричним відносно нуля. Це варто враховувати при програмуванні. Якщо, наприклад, змінити знак у найбільшого по модулю від’ємного числа, то виявиться, що отриманий результат не можна подати за допомогою тієї ж кількості розрядів.
Майже усі наші міркування були побудовані на базі 8-розрядних чисел. Але вони застосовні для чисел будь-якої розрядності. Від кількості розрядів k залежать лише граничні значення чисел, значення яких наведені в таблиці нижче.
| Розрядність | Мінімальне число | Максимальне число |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
Дробові числа
| Дробові числа в комп’ютері зберігаються у форматі з рухомою крапкою. Для назви розділення цілої і дробової частини числа використовують також термін «кома«, який і будемо використовувати далі у нашому записі чисел, пам’ятаючи, що в комп’ютері таким розділювачем використовується «крапка«. |
Наприклад, дробові числа -459,2 і 0,0000004592 у форматі з рухомою крапкою записуються так
-4,592E+02
4,592E-07де символ E читається як помножити на десять у степені (такий запис відображає експоненціальну форму запису числа).
Будь-яке дробове число r в експоненційальній формі записується у вигляді
r = ± m · npде m - мантиса числа, яка зберігає цифри числа, n - основа системи числення, p - порядок числа (ціле додатне або від’ємне число, яке вказує місце крапки в записі).
У десятковій системі такий запис використовують для позначення, наприклад, фізичних величин: швидкості світла у вакуумі
3 · 108 м/ссталої Больцмана
1,380649 · 10-23 Дж·К-1тощо.
Числа з рухомою крапкою можна подати різними способами, наприклад, для числа 34,5 будуть справедливі такі експоненціальні форми:
3450,0 · 10-2
345,0 · 10-1
34,5 · 100
3,45 · 101
0,345 · 102
0,0345 · 103Проте, запис чисел, в яких мантиса містить нулі перед десятковою крапкою (3450,0) чи після неї (0,0345) є не дуже хорошим варіантом, оскільки, зберігаючи ці нулі, збільшується розрядність чисел.
З практичної точки зору, більш зручно подавати число в експоненціальній формі, де ціла частина мантиси складається із єдиної ненульової цифри:
3,45 · 101В цьому випадку, мантиса повинна задовільняти умову:
1 ≤ m < nде n - основа системи числення. Таке подання дробових чисел в комп’ютері називають нормалізованим.
| Для нормалізованого запису числа нуль є своє правило: якщо і мантиса, і порядок рівні нулю, запис нуля є нормалізованим. |
Наведемо приклади нормалізації деяких дробових чисел:
31,41592610 = 3,141592610 · 101
0,0004510 = 4,510 · 10-4| В комп’ютерному поданні дробових чисел кількість цифр (розрядів) в мантисі визначає точність обчислень, з якою можна подати число, а кількість цифр (розрядів) для запису порядку - діапазон чисел. |
В різних типах комп’ютерів застосовуються різні варіанти подання дробових чисел у формі з рухомою крапкою. Для прикладу, розглянемо подання дробового числа в 4-байтовій комірці пам’яті.
4-байтовій комірці пам’ятіОтже, в комірці повинна зберігатися наступна інформація про число:
-
знак числа (зберігається в старшому біті і може мати значення:
0- позначає плюс,1- мінус); -
машинний порядок (машинний порядок зміщений відносно математичного порядку на певну величину і має лише додатні значення);
-
цифри мантиси.
Для нашого випадку, зв’язок між машинним порядком Mp і математичним p буде описуватися формулою:
Mp10 = p10 + 12710Ця формула записана в десятковій системі числення. У двійковій системі вона має такий вигляд:
Mp2 = p2 + 11111112Отже, у нашій ситуації для зберігання дробового числа необхідно виконати наступний алгоритм.
-
Перетворити модуль даного дробового числа у двійкову систему числення.
-
Нормалізувати двійкове число.
-
Знайти машинний порядок в двійковій системі числення.
-
Враховуючи знак числа, записати його подання в
4-байтовому машинному слові.
Запишемо подання в пам’яті дробового від’ємного числа -13,37510 у формі з рухомою крапкою, використовуючи даний алгоритм.
-
Перетворити модуль дробового числа
-13,37510у двійкову систему числення:
13,37510 = 1101,0112-
Записати експоненціальний запис двійкового числа у нормалізованій формі:
1101,0112 = 1,1010112 · 10211В цьому записі мантиса 1,101011, основа системи числення (210 = 102) і порядок (310 = 112) записані у двійковій системі.
Ціла частина мантиси в нормалізованому вигляді дорівнює 1 і не входить до коду числа. Це, так звана, прихована одиниця, яка не зберігається в пам’яті, як наслідок, це економія одного розряду. На місце мантиси записується хвіст мантиси - всі дробові цифри мантиси (крім першої одиниці, яка є цілою частиною).
|
-
Обчислити машинний порядок у десятковій формі:
Mp10 = 310 + 12710 = 13010У двійковій формі машинний порядок матиме вигляд:
13010 = 100000102| На відміну від цілих чисел, мантиса дробових чисел зберігається в прямому коді. Таким чином, мантиси додатного і, рівного за модулем, від’ємного числа однакові, а відрізняються вони лише старшим (знаковим) бітом. |
-
Записати двійкове подання числа в
4-байтовій комірці пам’яті з урахуванням знаку числа:
1 10000010 101011000000000000000002Прогалини у двійковому коді поставлені тільки для зручності читання і відокремлюють знаковий біт від машинного порядку, а машинний порядок - від мантиси.
Отримаємо більш компактний запис в шістнадцятковій системі:
C156000016Розв’яжемо обернену задачу. Визначимо десяткове представлення дробового числа за шістнадцятковим поданням 41C4000016.
Перетворимо шістнадцяткове число 41C4000016 у двійкову систему і розділимо пропуски по чотири розряди для кращого читання:
41C4000016 = 0100 0001 1100 0100 0000 0000 0000 00002А тепер розтавимо пропуски так, щоб відділити знаковий біт від машинного порядку, а машинний порядок - від мантиси:
0 10000011 100010000000000000000002Число додатне, так як в знаковому розряді присутній нуль.
Машинний порядок числа має значення 100000112. Перетворимо це двійкове число в десяткову cистему числення
100000112 = 13110і визначимо математичний порядок числа
13110 - 12710 = 410Мантиса числа 100010000000000000000002, отже, нормалізована мантиса
1,100010000000000000000002Шукане число в нормалізованій формі
1,10001 · 24або ж, якщо використовувати повністю двійковий запис для основи системи числення (210 = 102) і порядку (410 = 1002)
1,10001 · 10100Записавши без мантиси і перенісши крапку на чотири розряди вправо, отримаємо двійкове значення, після перетворення якого в десяткову систему числення, матимемо значення дробового числа
11000,12 = 24,510Додаток B: Числа в Python
Цілі числа
Python підтримує десяткові, двійкові, вісімкові та шістнадцяткові цілі числа, причому не накладається ніяких обмежень на величину (довжину) числа, головне, щоб вистачало пам’яті для зберігання таких чисел.
Десяткові цілі числа створюються за допомогою десяткових цифр:
0
7
168
44601490397061246283071436545296723011960832Двійкові числа складаються з префікса 0b (або 0B) і двійкових цифр 0 і 1:
>>> 0b0
0
>>> 0b1
1
>>> 0b10
2
>>> 0b100
4
>>> 0b111
7
>>> 0b10011001
153
>>> 0B100001
33Вісімкові числа починаються з префікса 0o (0O) і можуть містити тільки цифри 0, 1, 2, 3, 4, 5, 6, 7:
>>> 0o0
0
>>> 0o1
1
>>> 0o12
10
>>> 0o45
37
>>> 0o2021
1041Шістнадцяткові числа починаються з префікса 0x (0X) і можуть містити як всі десяткові цифри, так і символи латинського алфавіту: a, b, c, d, e, f (або A, B, C, D, E, F), які в даному випадку виступають в ролі чисел:
>>> 0x0
0
>>> 0x15
21
>>> 0xD4
212
>>> 0xab4
2740
>>> 0xC1
193
У мовах програмування із суворою типізацією необхідно вказувати як тип числа, так і те, що створюваний об’єкт сам є числом. Але в Python такої необхідності немає, інтерпретатор Python сам, на основі аналізу літералів чисел, здатний зрозуміти, що перед ним: число або ні, ціле або з рухомою крапкою, двійкове або шістнадцяткове тощо.
|
Розглянемо підтримку цілих чисел у Python і на практиці подивимось, як створюються цілі числа.
В інтерактивному інтерпретаторі Python запишемо інструкцію:
>>> a = 39У загальному випадку, в мові програмування, даний запис можна прочитати так: змінній a присвоїти цілочисельне значення 39 . Символом = тут позначається оператор присвоєння.
Змінні в Python - імена-посилання на об’єкти.
|
Тобто, у записі a = 39, a - посилання на об’єкт (екземпляр класу int) - ціле число 39.
Виконаємо ще одне «присвоєння»:
>>> b = aЗапис b = a змушує ім’я b посилатися на той самий об’єкт, що і ім’я a. Перевіримо це твердження:
>>> a is b
True
Операція a is b перевіряє, чи вказують обидва імені на один і той же об’єкт.
|
Оператор is перевіряє об’єкти на ідентичність:
-
x is yбуде істиною, якщоxіyє одним і тим же об’єктом; -
також можна використовувати конструкцію
is not, наприклад,x is not yбуде істиною, якщоxіyє різними об’єктами.
PEP8 рекомендує використовувати оператор is для порівняння з об’єктами, що існують в єдиному екземплярі, наприклад, для None.
|
if foo is not None:
passПеревірку на ідентичність можна виконати також за допомогою функції id():
>>> id(a) == id(b)
True
>>> id(a)
140713044069216
>>> id(b)
140713044069216
Функція id() повертає унікальний ідентифікатор для зазначеного об’єкта. Ідентифікатор - це ціле число, яке гарантовано є унікальним та постійним для цього об’єкта протягом його життя (від моменту створення і до моменту знищення об’єкта). Для порівняння ідентифікаторів об’єктів ми використали оператор порівняння ==.
|
Проілюструємо вищенаведені відомості ще на одному прикладі.
>>> a = 3
>>> b = 3
>>> id(3) == id(a) == id(b)
True
>>> id(3)
140713044068064
>>> id(a)
140713044068064
>>> id(b)
140713044068064
>>> c = 257
>>> d = 257
>>> id(257) == id(c) == id(d)
False
>>> id(257)
1980287707152
>>> id(c)
1980287707408
>>> id(d)
1980287707120
>>>Ідентичність об’єкта асоціюється з адресою об’єкта в пам’яті (для реалізації CPython - найбільш поширена, еталонна реалізація інтерпретатора мови програмування Python, яку ми, власне, і завантажуємо із офіційного сайта) і буде різною для кожного запуску, окрім деяких об’єктів, які мають постійний унікальний ідентифікатор, таких, як цілі числа від -5 до 256 включно.
Коли ви створюєте об’єкт типу int у цьому діапазоні, ви, фактично, просто отримуєте посилання на вже існуючий об’єкт, а не на новий об’єкт. А от, наприклад, для числа 257 буде створений новий об’єкт.
Усі цілі числа у Python реалізуються як довгі цілі об’єкти довільної величини .
|
Інтерпретатор Python оптимізований так, що невеликі цілі числа представлені одним об’єктом - це зроблено з метою поліпшення продуктивності. Для великих чисел це вже не виконується.
Інші реалізації Python, такі як Jython або IronPython, можуть мати іншу реалізацію функції id(). Тому, наведені вище приклади є особливостями реалізації інтерпретатора, а не мовною особливістю Python.
У стандартній реалізації CPython (написаний на мові C ) є багато заздалегідь визначених об’єктів, включаючи кілька малих цілих чисел та кілька одиничних символів ASCII .
|
Реальний код повинен бути незалежним від деталей реалізації. Тому, для порівняння чисел, не варто використовувати перевірку на ідентичність (різні об’єкти можуть мати одне значення). Використовуйте a == b, щоб дізнатися чи рівні числа. Наприклад:
>>> x = 39
>>> y = 39
>>> x == y # має бути два різних об'єкти з однаковими значеннями: порівняння
True
>>> x is y # той самий об'єкт: кешування
True
>>>У цьому прикладі змінні x і y повинні бути рівні (==, одне і те ж значення), але не еквівалентні (is, один і той же об’єкт). Однак, через те, що малі цілі числа і рядки кешуються і використовуються повторно, оператор is повідомляє, що імена-змінні посилаються на один і той же об’єкт.
Отже, коли ви «запитаєте» Python, чи дійсно -5 is -5, це, безумовно, буде True, тому що обидва екземпляри є одним і тим же екземпляром, тоді, як поза діапазоном [-5, 256], CPython може створювати і, ймовірно, створює нові екземпляри цілих чисел.
Проілюструємо наші міркування на прикладі.
>>> a = 257
>>> b = 257
>>> a is b
False
>>> id(a) == id(b)
False
>>> id(a)
1624253033232
>>> id(b)
1624253032464
>>> 257 is 257
<stdin>:1: SyntaxWarning: "is" with a literal. Did you mean "=="?
True
>>> id(257) == id(257)
True
>>>Чому 257 is 257 дає значення True? Це пов’язано з тим, що Python виконує цю інтерактивну інструкцію як єдиний блок (в реалізації CPython). Під час інтерпретації цього твердження, CPython «побачить», що у вас є два однакові літерали і буде використовувати одне і те ж представлення 257.
Наприкінці, розглянемо ще одну особливість виконання коду в інтерактивному режимі інтерпретатора CPython:
>>> id(333)
2609261210384
>>> id(334)
2609261210384
>>> id(335)
2609261210384
>>> id(333), id(334), id(335)
(2609261210384, 2609261209872, 2609231362288)Такі результати можна пояснити, звернувшись до документації Python для функції id().
Два об’єкти з періодами життя, що не перекриваються, можуть мати однакове значення id() .
|
Іншими словами, оскільки ми не зберігаємо жодних посилань на ціле число 333, його об’єкт видаляється з пам’яті після друку в інтерактивному режимі інтерпретатора.
Потім ми створюємо об’єкт 334, і йому видається така сама адреса в пам’яті. Так як немає посилань на ціле число 334, його об’єкт також видаляється з пам’яті. При створенні об’єкта 335 йому знову видається та сама адреса в пам’яті і т.д.
При виконанні інструкцій єдиним блоком, ми спотерігаємо різні значення id для поданих цілих об’єктів.
Числа з рухомою крапкою
У Python, головною відмінністю дробових чисел від цілих є наявність символу крапки . (не коми, як ми звикли записувати), яка відділяє цілу частину від дробової. Тому запис десяткових дробових чисел у Python буде таким:
3.5
6.0
6.
0.24
.24Якщо Python бачить, що зліва чи справа від крапки нічого немає, то він розуміє, що або ціла, або дробова частина дорівнює 0.
Такий запис десяткового дробового числа називається класичним або з фіксованою крапкою.
Іншою відмінною рисою, зокрема для запису дуже великих або дуже маленьких за модулем дробових чисел, є використання формату з рухомою крапкою.
У цьому випадку число представляється у вигляді деякого десяткового дробового числа (мантиса), яке помножене на 10 (основа системи числення) в деякому степені (порядок).
Наприклад, у фізиці, маса електрона (у кг) записується у форматі з рухомою крапкою так:
9.1 · 10-31У Python числа з рухомою крапкою записуюються у вигляді мантиси, потім пишеться буква e (експонента), потім пишеться порядок. Пропуски всередині цього запису не ставляться. Перед самим числом також може стояти знак мінус -. Наприклад, маса електрона (в кг) у Python може бути записана у форматі з рухомою крапкою так:
9.1e-31Cтандартним типом у мові програмування Python, який використовується для представлення дробових чисел - це float. Якщо на довжину цілих чисел не накладається абсолютно ніяких обмежень по величині, то з дробовими числами це не так.
Щоб дізнатися інформацію про числа типу float для комп’ютера, на якому відкритий інтерактивний режим інтерпретатора Python, можна скористатися такими командами:
>>> import sys
>>> sys.float_info # виведення відформатовано вручну
sys.float_info(max=1.7976931348623157e+308, (1)
max_exp=1024, (2)
max_10_exp=308, (3)
min=2.2250738585072014e-308, (4)
min_exp=-1021, (5)
min_10_exp=-307, (6)
dig=15, (7)
mant_dig=53, (8)
epsilon=2.220446049250313e-16, (9)
radix=2, (10)
rounds=1) (11)-
max- максимальне число для подання. -
max_exp- максимальна степінь двійки. -
max_10_exp- максимальне числоe, таке, що 10 у степені e знаходиться в діапазоні[min, max]. -
min- мінімальне число для подання. -
min_exp- мінімальна степінь двійки. -
min_10_exp- мінімальне числоe, таке, що 10 у степені e знаходиться в діапазоні[min, max]. -
dig- максимальне число цифр, якими можна точно відобразити число. -
mant_dig- максимальне число цифр вradix-системі числення, якими можна точно відобразити число. -
epsilon- різниця між1і найменшим числом (більшим за1), яку можна подати як число з рухомою крапкою. -
radix- основа системи числення, що використовується. -
rounds- цілочисельна константа, яка визначає режим округлення.
У наступному прикладі показано допустиме подання числа і вихід за межі типу float у Python:
>>> 10.0**308
1e+308
>>> 10.0**309
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
OverflowError: (34, 'Result too large')Як бачимо, Python генерує виняток OverflowError. Цей виняток виникає, коли результат арифметичної операції занадто великий для його подання. Він не з’являється при звичайній роботі з цілими числами, так як Python підтримує «довгі числа».
Проте, замість помилок OverflowError, коли число виходить за вказані межі, іноді з’являються значення -inf і inf:
>>> 1.7e+308 * 1.7e+308
inf
>>> -1.7e+308 * 1.7e+308
-infЗначення -inf і inf - це не що інше, як числа, що позначають -/+ нескінченність. Це також числа з рухомою крапкою, які можуть брати участь в обчисленнях:
>>> a = 10e555
>>> a
inf
>>> a * 100
inf
>>> a - 100
infОднак, що б ви не робили з нескінченністю, вона так і залишиться нескінченністю. Єдине, що можна спробувати, так це відняти від однієї нескінченності іншу нескінченність:
>>> a = 10e555
>>> b = 10e554
>>> a
inf
>>> b
inf
>>> c = a - b
>>> c
nan
nan - значення, яке означає не число (Not-a-Number) - одне з особливих значень числа з рухомою комою. Проте, значення nan поводиться як число, і, якщо воно з’явиться у деякому виразі, результат завжди буде nan (окрім операції nan/0, яка генерує помилку ділення на нуль).
|
>>> c + 50
nan
>>> c * a * b
nan
>>> c / 0
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ZeroDivisionError: float division by zeroОкрім обмеженого діапазану значень, у чисел з рухомою крапкою є ще одна проблема, яка пов’язана з їх поданням в пам’яті комп’ютера.
Числа з рухомою крапкою представлені в комп’ютерних апаратних системах як дроби з основою 2 (двійкова система числення). Наприклад, якщо десятковий дріб 0.125 має значення
1/10 + 2/100 + 5/1000то, таким же чином, двійковий дріб 0.001 має значення
0/2 + 0/4 + 1/8Ці два дроби мають однакові значення і відрізняються лише тим, що перший записаний в дробовому вигляді за основою 10, а другий - за основою 2.
| Більшість десяткових дробів не можуть бути точно представлені в двійковому записі. Наслідком цього є те, що, в основному, десяткові дробові числа є тільки наближеними до двійкових, які і зберігаються в пам’яті комп’ютера. |
Проблему легше зрозуміти на прикладі десяткової системи числення.
Розглянемо дріб 1/3. Його можна записати десятковим дробом
0.3або
0.33або
0.333і т. д. Незалежно від того, як багато цифр ви запишете, результат ніколи не буде точно дорівнювати 1/3, але буде все більш кращим наближенням до 1/3.
Аналогічно, у двійковій системі числення, не має значення, як багато цифр з основою 2 ви будете використовувати, десяткове значення 0.1 не може бути представлено точно в двійковому записі дробу. За основою 2 десятковий дріб 1/10 - це нескінченно повторюваний дріб.
0.0001100110011001100110011001100110011001100110011(0011)Якщо зупинитись на будь-якій кінцевій кількості біт, це приведе до отримання наближення.
У мові Python стандартний тип float має подвійну точність, тобто зберігається у вигляді 64-бітного рядка.
|
Python виводить тільки десяткове наближення справжнього десяткового значення від двійкового наближення, що зберігається в пам’яті комп’ютера. На більшості комп’ютерів, якби Python виводив десяткове значення двійкового наближення числа 0.1, то результат міг би бути, наприклад, таким (використано рядкове форматування):
>>> f'{0.1:.55f}'
'0.1000000000000000055511151231257827021181583404541015625'Але Python дозволяє керувати кількістю цифр, відображаючи округлене значення:
>>> 1/10
0.1
Якщо, навіть, результат виглядає як точне значення 1/10, то, насправді, збережене значення - це найближче представлення двійкового дробу.
|
Такі наближення можуть породжувати цікаві ситуації при обчисленнях в Python. Наприклад, оскільки 0.1 не є точним значенням 1/10, сума трьох значень 0.1 не дорівнює точно 0.3:
>>> 0.1 + 0.1 + 0.1 == 0.3
FalseТакож, оскільки 0.1 не може наблизитися до точного значення 1/10 і 0.3 не може наблизитися до точної величини 3/10, то попереднє округлення за допомогою функції round(), вбудованої в Python, не допомагає:
>>> round(.1, 1) + round(.1, 1) + round(.1, 1) == round(.3, 1)
False
Округлення в Python здійснюється вбудованою функцією round(number, digits), де number - число, яке округлюється, а digits - кількість знаків після крапки.
|
Хоча числа не можуть бути наближені до їх точних значень, функція round() може бути корисною для округлення результату обчислень:
>>> round(.1 + .1 + .1, 10) == round(.3, 10)
TrueРозглянемо ще кілька прикладів подання чисел з рухомою крапкою в Python, використовуючи рядкове форматування:
>>> f'{2.55:.30f}'
'2.549999999999999822364316059975'
>>> f'{2.65:.30f}'
'2.649999999999999911182158029987'
>>> f'{2.75:.30f}'
'2.750000000000000000000000000000'
>>> f'{2.85:.30f}'
'2.850000000000000088817841970013'
>>> f'{2.5:.30f}'
'2.500000000000000000000000000000'
>>> f'{1.5:.30f}'
'1.500000000000000000000000000000'
>>> f'{8.45:.30f}'
'8.449999999999999289457264239900'Застосуємо до чисел, поданих вище, округлення за допомогою функції round():
>>> round(2.55, 1)
2.5
>>> round(2.65, 1)
2.6
>>> round(2.75, 1)
2.8
>>> round(2.85, 1)
2.9
>>> round(2.5)
2
>>> round(1.5)
2
>>> round(8.45, 1)
8.4Такі результати округлення можуть говорити про те, що Python (версій 3.x.x) використовує різні правила для округлення.
Щоб з’ясувати, яке округлення використовується, потрібно поглянути на запис числа з великою кількістю знаків після крапки:
-
якщо число в машинному поданні не точно представляється, то округлення відбувається до найближчого числа;
-
якщо число в машинному поданні точно представляється, то використовується банківське округлення - округлення до найближчого парного.
Для боротьби з несподіваними результатами арифметичних обчислень, коли вимагається точність обчислень, рекомендується використовувати бібліотеку decimal.
|
Для випадків, які вимагають точного десяткового подання, спробуйте використовувати модуль decimal , який реалізує десяткову арифметику і підходить для бухгалтерських і високоточних обчислень. Інша форма точної арифметики підтримується модулем fractions , який реалізує арифметику, засновану на раціональних числах (тобто, числа подібні Якщо ви часто використовуєте операції з рухомою крапкою, вам слід поглянути на пакунки для математичних і статистичних операцій, що надаються проектом scipy.org . |
Приклад використання модуля decimal
n = int(input()) # кількість знаків після крапки
from decimal import Decimal, ROUND_HALF_UP
e = Decimal('2.7182818284590452353602875')
print(e.quantize(Decimal('1.'+n*'0'), ROUND_HALF_UP))коли необхідно виконати математичне округлення до вказаної кількості знаків після крапки:
19
2.7182818284590452354
Стандартно, максимальне число цифр після крапки, якими можна точно відобразити дробове число у Python - 15. Модуль decimal допоміг математично правильно округлити число 2.7182818284590452353602875 до 19 знаків після крапки.
|
Python надає інструменти (методи), які можуть допомогти в тих рідкісних випадках, коли ви справді хочете дізнатися точне значення дробового числа.
Наприклад, метод as_integer_ratio() подає значення дробового числа як дріб (повертає пару цілих чисел (кортеж), перше з яких дорівнює чисельнику, а друге - завжди додатному знаменнику звичайного дробу, значення якого точно співпадає з вхідним числом типу float):
>>> x = 0.7
>>> x.as_integer_ratio()
(3152519739159347, 4503599627370496)Оскільки це співвідношення точне, воно може бути використано, щоб без втрат відтворити початкове значення:
>>> x == 3152519739159347 / 4503599627370496
TrueПоява таких великих чисел пов’язане з тим, що числа типу float, насправді, не є десятковими дробами, і зберігаються в пам’яті з невеликою похибкою:
>>> from decimal import *
>>> Decimal(3152519739159347) / Decimal(4503599627370496)
Decimal('0.6999999999999999555910790150')За допомогою модулів decimal і fractions можна легко керувати точністю подання чисел в Python. В наступному прикладі, метод from_float() будує точне значення числа типу float:
>>> from decimal import *
>>> from fractions import *
>>> x = 1.8
>>> Decimal.from_float(x)
Decimal('1.8000000000000000444089209850062616169452667236328125')
>>> Fraction.from_float(x)
Fraction(8106479329266893, 4503599627370496)
>>> 8106479329266893 / 4503599627370496
1.8
>>> f'{Decimal.from_float(x):.17f}'
'1.80000000000000004'Python дозволяє перетворювати числа з рухомою крапкою з десяткової системи числення в шістнадцяткову і навпаки. Для цього використовуються методи hex() і fromhex() відповідно:
>>> float.hex(4.56789)
'0x1.24584f4c6e6dap+2'
>>> float.fromhex('0x1.24584f4c6e6dap+2')
4.56789Створення чисел з рухомою крапкою з їх шістнадцяткового подання дозволяє уникнути похибки, яка неминуче виникає при перетворенні десяткових дробових чисел у двійкову систему числення.
Шістнадцяткові числа з рухомою крапкою в Python задаються рядком виду
[sign] ['0x'] integer ['.' fraction] ['p' exponent]в якому:
-
sign- необов’язковий знак, який може бути як+або-; -
integerіfraction- ціла і дробова частини, які повинні обов’язково містити хоча б по одній цифрі; -
'0x'- префікс, що позначає шістнадцяткові числа; -
'p' exponent- експонента у вигляді десяткового цілого числа зі знаком чи без (показник степеня'p' exponentє степенем двійки).
Наприклад, перетворення числа '0x2.f1ap+3' з шістнадцяткової системи числення в десяткову буде виглядати наступним чином:
>>> (2 + 15./16 + 1./16**2 + 10./16**3)*2**3
23.55078125Застосування зворотного перетворення дає інший шістнадцятковий рядок, який, однак, представляє те ж саме число:
>>> float.hex(23.55078125)
'0x1.78d0000000000p+4'
>>> (1 + 7./16 + 8./16**2 + 13./16**3)*2**4
23.55078125